

Nächste Seite: Schätzverfahren
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Anmerkungen zur Schätztheorie
Bei unseren statistischen Berechnungen schätzen wir öfter als uns
bewußt ist. So ``berechnen`` wir den Mittelwert von Zeitreihen und fassen
diesen Stichprobenmittelwert als Mittelwert der zu untersuchenden Variable
(Grundgesamtheit) auf. Man kann zeigen, daß dieses Momentenschätzverfahren
in einem gewissen Sinn gut sein kann. Da es aber durchaus Fälle gibt, in
denen es ganz extrem schlecht sein kann, sollte man sich bewußt machen, was
man tut, wenn man berechnete Kenngrößen von Zeitreihen als Eigenschaften der
zugrunde liegenden Variablen interpretiert. Dazu ein Beispiel:
Um zu testen, ob ein Residuum weitere Information enthält, testet man es auf
Gaußverteilung. Dazu paßt man zunächst eine Gaußverteilung an, indem man
die Stichprobenvarianz und den Stichprobenmittelwert als Parameter der
anzupassenden Gaußverteilung verwendet. In einem zweiten Schritt, testet man
(z.B. mit dem 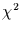 - oder dem Kolmogoroff-Smirnoff-Test) ob die
angepaßte Gaußverteilung gut paßt. Wenn dem so ist, ist man fertig. Nun
könnte aber eine andere ähnliche Verteilung auch gut passen. Das wäre
nicht schlimm, wenn nicht verschiedene (auch offensichtlich ähnliche)
Verteilungen auf ganz unterschiedlichen Modellvorstellungen beruhen könnten,
die zu ganz unterschiedlichen Interpretationen Anlaß geben. So sehen z.B. die
Ableitung der Fermi-Funktion (FV) und die Cauchy-Verteilung (CV) der
Gauß-Verteilung (GV) sehr ähnlich. Während aber die Gauß-Verteilung aus
der Summe vieler Zufallsvariablen resultiert (zentraler Grenzwertsatz) und
damit
als reines additives Rauschen angesehen werden kann, ist die Cauchy-Verteilung
das Verhältnis aus zwei Gauß-verteilten Variablen. Der Unterschied wird
darin deutlich, daß der Mittelwert einer Realisation einer (normierten)
Gauß-verteilten Variable gegen den Mittelwert der Grundgesamtheit der
Variablen (und der ist 0) konvergiert, während der Mittelwert einer
Cauchy-verteilten Variablen divergiert, d.h. mit zunehmender Stichprobenlänge
immer größer wird. Der Erwartungswert der Cauchy-Verteilung ist
unendlich. Die Fermi-Verteilung, die der Gauß-Verteilung sehr ähnlich sieht,
hat den Vorteil, daß sie analytisch integrierbar ist. Durch diese Eigenschaft
ist sie für viele praktische Anwendungen der Gauß-Verteilung überlegen.
Als Fazit dieser Ausführungen bleibt festzuhalten, daß es sich lohnt, sich
mit der Frage zu beschäftigen, wie man Parameter und damit
Modellvorstellungen schätzt.
- oder dem Kolmogoroff-Smirnoff-Test) ob die
angepaßte Gaußverteilung gut paßt. Wenn dem so ist, ist man fertig. Nun
könnte aber eine andere ähnliche Verteilung auch gut passen. Das wäre
nicht schlimm, wenn nicht verschiedene (auch offensichtlich ähnliche)
Verteilungen auf ganz unterschiedlichen Modellvorstellungen beruhen könnten,
die zu ganz unterschiedlichen Interpretationen Anlaß geben. So sehen z.B. die
Ableitung der Fermi-Funktion (FV) und die Cauchy-Verteilung (CV) der
Gauß-Verteilung (GV) sehr ähnlich. Während aber die Gauß-Verteilung aus
der Summe vieler Zufallsvariablen resultiert (zentraler Grenzwertsatz) und
damit
als reines additives Rauschen angesehen werden kann, ist die Cauchy-Verteilung
das Verhältnis aus zwei Gauß-verteilten Variablen. Der Unterschied wird
darin deutlich, daß der Mittelwert einer Realisation einer (normierten)
Gauß-verteilten Variable gegen den Mittelwert der Grundgesamtheit der
Variablen (und der ist 0) konvergiert, während der Mittelwert einer
Cauchy-verteilten Variablen divergiert, d.h. mit zunehmender Stichprobenlänge
immer größer wird. Der Erwartungswert der Cauchy-Verteilung ist
unendlich. Die Fermi-Verteilung, die der Gauß-Verteilung sehr ähnlich sieht,
hat den Vorteil, daß sie analytisch integrierbar ist. Durch diese Eigenschaft
ist sie für viele praktische Anwendungen der Gauß-Verteilung überlegen.
Als Fazit dieser Ausführungen bleibt festzuhalten, daß es sich lohnt, sich
mit der Frage zu beschäftigen, wie man Parameter und damit
Modellvorstellungen schätzt.


Nächste Seite: Schätzverfahren
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Anmerkungen zur Schätztheorie
ich
2000-01-24