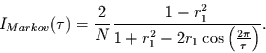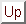


Nächste Seite: Über dieses Dokument ...
Aufwärts: Anwendungen
Vorherige Seite: Anderson-Darling-Test
Inhalt
Der einfachste stochastische Prozeß ist das weiße Rauschen, das besagt, daß
keine Information von Zeitreihenwert zu Zeitreihenwert weitergegeben wird.
Im zweiteinfachsten Fall wird ein Anteil 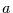 der Information immer genau einen Zeitschritt weitergegeben, d.h.
der Information immer genau einen Zeitschritt weitergegeben, d.h.
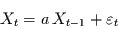 |
(2.17) |
wobei
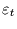 ein weißes Rauschen darstellt. Ein solcher Prozeß
wird autoregressiver Prozeß erster Ordnung (AR(1)-Prozeß,
aber auch Markov-Prozeß) genannt, eben
weil die Information autoregressiv um einen Zeitschritt weitergegeben wird.
Der Prozeß erscheint physikalisch sehr plausibel, denn die Zukunft hängt
dann nur vom momentanen Wert und einer Übergangswahrscheinlichkeit ab, nicht
aber davon wie der momentane Wert erreicht wurde.
Wenn der Anteil
ein weißes Rauschen darstellt. Ein solcher Prozeß
wird autoregressiver Prozeß erster Ordnung (AR(1)-Prozeß,
aber auch Markov-Prozeß) genannt, eben
weil die Information autoregressiv um einen Zeitschritt weitergegeben wird.
Der Prozeß erscheint physikalisch sehr plausibel, denn die Zukunft hängt
dann nur vom momentanen Wert und einer Übergangswahrscheinlichkeit ab, nicht
aber davon wie der momentane Wert erreicht wurde.
Wenn der Anteil 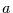 um einen Zeitschritt weitergegeben wird und davon
wieder der gleiche Anteil noch einen Zeitschritt weiter, so wird der Anteil
um einen Zeitschritt weitergegeben wird und davon
wieder der gleiche Anteil noch einen Zeitschritt weiter, so wird der Anteil
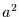 zwei Zeitschritte weiter gegeben und allgemein der Anteil
zwei Zeitschritte weiter gegeben und allgemein der Anteil
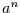 um
um 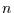 Zeitschritte. Ein solcher Prozeß hat demnach eine
Autokorrelationsfunktion von
Zeitschritte. Ein solcher Prozeß hat demnach eine
Autokorrelationsfunktion von 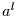 , wenn
, wenn 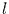 die Verschiebung (Lag) ist.
Man kann sich nun die Frage stellen, ob die betrachtete Zeitreihe die
Realisation eines solchen Prozesses (möglicherweise mit überlagerten
Schwingungen, die dann wegen der Linearität des Prozesses nicht
frequenzverzerrt sind) ist, d.h.:
die Verschiebung (Lag) ist.
Man kann sich nun die Frage stellen, ob die betrachtete Zeitreihe die
Realisation eines solchen Prozesses (möglicherweise mit überlagerten
Schwingungen, die dann wegen der Linearität des Prozesses nicht
frequenzverzerrt sind) ist, d.h.:
![\begin{displaymath}
X_{t}=aX_{t-1}+\varepsilon_{t}+\sum_{i=1}^{m}[A_{i}\cos(2\pi\omega_{i}t)+B_{i}\sin(2\pi\omega_{i}t)].
\end{displaymath}](img189.gif) |
(2.18) |
Falls die Schwingungen nun wesentlich zur Varianz beitragen,
sieht man sie in der Zeitreihe mit bloßem Auge. Ist dies nicht der Fall, so
ist der Wert der Autokorrelation der Zeitreihe zur Verschiebung eins
(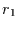 ) ein guter Schätzwert für
) ein guter Schätzwert für 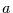 . Kennt man aber
. Kennt man aber 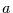 so kennt man
den Prozeß, wie er ohne die Schwingungen währe. Das Spektrum hätte dann
folgende Form:
so kennt man
den Prozeß, wie er ohne die Schwingungen währe. Das Spektrum hätte dann
folgende Form:
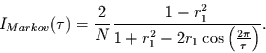 |
(2.19) |
Selbst wenn nun 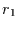 ein guter Schätzer für
ein guter Schätzer für 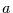 ist (was bedingt, daß
die Störungen gegenüber dem reinen Markov-Prozeß klein sind) und die
Zeitreihe tatsächlich aus einem Markov-Prozeß stammt, muß das
Zeitreihenspektrum (auch das geglättete) nicht so aussehen. Nun kann man
aber versuchen zu testen, ob das Zeitreihenspektrum ganz und gar nicht mit
der Hypothese verträglich ist. Dazu genügt es die Konvidenzintervalle
des theoretisch zugeordneten Spektrums zu kennen, d.h. die Wahrscheinlichkeit,
mit der ein bestimmter Spektralwert weiter als ein bestimmter Wert vom
theoretischen Spektrum abweicht. Es muß also nun der zu einer vorgegebenen
Wahrscheinlichkeit größte Abstand gesucht werden (d.h. das
Konfidenzintervall). Der Unterschied dieses Tests zum obigen White-Noise-Test
ist der, daß hier eine unzuverlässigere Variable (nämlich der
spektrale Wert, statt dem kumulativen spektralen Wert) getestet wird. Diese
ist nach Panofsky und Brier (1958)
ist (was bedingt, daß
die Störungen gegenüber dem reinen Markov-Prozeß klein sind) und die
Zeitreihe tatsächlich aus einem Markov-Prozeß stammt, muß das
Zeitreihenspektrum (auch das geglättete) nicht so aussehen. Nun kann man
aber versuchen zu testen, ob das Zeitreihenspektrum ganz und gar nicht mit
der Hypothese verträglich ist. Dazu genügt es die Konvidenzintervalle
des theoretisch zugeordneten Spektrums zu kennen, d.h. die Wahrscheinlichkeit,
mit der ein bestimmter Spektralwert weiter als ein bestimmter Wert vom
theoretischen Spektrum abweicht. Es muß also nun der zu einer vorgegebenen
Wahrscheinlichkeit größte Abstand gesucht werden (d.h. das
Konfidenzintervall). Der Unterschied dieses Tests zum obigen White-Noise-Test
ist der, daß hier eine unzuverlässigere Variable (nämlich der
spektrale Wert, statt dem kumulativen spektralen Wert) getestet wird. Diese
ist nach Panofsky und Brier (1958) 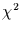 -verteilt. Man erhält das
Konfidenzintervall demnach gegeben durch
-verteilt. Man erhält das
Konfidenzintervall demnach gegeben durch
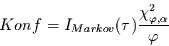 |
(2.20) |
mit der Irrtumswahrscheinlichkeit 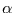 (d.h.
(d.h. 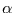 ist die
Wahrscheinlichkeit dafür, daß
das Konfidenzintervall durch Zufall überschritten
wird) und dem Freiheitsgrad
ist die
Wahrscheinlichkeit dafür, daß
das Konfidenzintervall durch Zufall überschritten
wird) und dem Freiheitsgrad 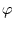 , der von der Anzahl der verwendeten
Fourier-Frequenzen
, der von der Anzahl der verwendeten
Fourier-Frequenzen 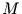 und der Zeitreihenlänge
und der Zeitreihenlänge 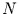 abhängt:
abhängt:
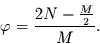 |
(2.21) |
Für die Anwendung hier (mit 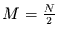 ) folgt
daraus
) folgt
daraus
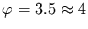 .
Die Konfidenzlevels
.
Die Konfidenzlevels 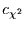 der
der 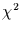 -Verteilung
können (mit Hilfe der Cornish-Fisher-Entwicklung)
aus denen der Gauß-Verteilung
-Verteilung
können (mit Hilfe der Cornish-Fisher-Entwicklung)
aus denen der Gauß-Verteilung 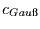 wie folgt berechnet werden:
wie folgt berechnet werden:
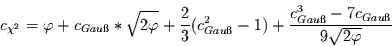 |
(2.22) |
mit:
Bei aller Vorsicht kann man mit diesem Test auch das weiße Spektrum
(d.h. das nicht kumulative) auf überzufällige Peaks testen. Der Vorteil
gegenüber dem obigen Test liegt darin, daß man bestimmte Peaks
verantwortlich für die Nichtübereinstimmung machen kann, der Nachteil ist,
daß das Ergebnis zweifelhaft ist.



Nächste Seite: Über dieses Dokument ...
Aufwärts: Anwendungen
Vorherige Seite: Anderson-Darling-Test
Inhalt
ich
2000-01-25