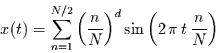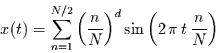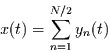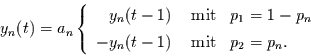Nächste Seite: Literatur
Aufwärts: Mögliche physikalische Ursachen für
Vorherige Seite: Fehlende räumliche Skala
Inhalt
Schon in Kapitel 7 wurde gezeigt, daß man mit den Weierstraßschen
Sinusfunktionen ein 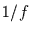 -Spektrum erzeugen kann. Wir können also von
-Spektrum erzeugen kann. Wir können also von
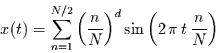 |
(63) |
ausgehen. Ohne die Struktur des Spektrums zu verändern
(s. [10]) können wir statt der Sinusfunktionen auch die
Rademacherfunktionen
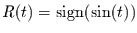 , also eine Funktion die zwischen
plus und minus eins springt, verwenden. Dann kann
, also eine Funktion die zwischen
plus und minus eins springt, verwenden. Dann kann
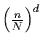 als Sprungamplitude aufgefaßt werden und
die Rademacherfunktion als Sprunghäufigkeit mit dieser Amplitude. Dabei
springt die Rademacherfunktion
als Sprungamplitude aufgefaßt werden und
die Rademacherfunktion als Sprunghäufigkeit mit dieser Amplitude. Dabei
springt die Rademacherfunktion
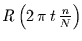 mit der Wahrscheinlichkeit 1 im
Intervall 0 bis
mit der Wahrscheinlichkeit 1 im
Intervall 0 bis 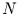 mit der Häufigkeit
mit der Häufigkeit
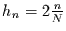 . Nun kann man
ohne das Spektrum zu beeinflussen, diese Häufigkeit als
Sprungwahrscheinlichkeit
. Nun kann man
ohne das Spektrum zu beeinflussen, diese Häufigkeit als
Sprungwahrscheinlichkeit 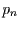 eines Poisson-Prozesses auffassen. Man kann
dann keine Aussage mehr über den Zeitpunkt der Sprünge machen, nur über die
Wartezeit auf Sprünge bestimmter Amplitude. Der Erwartungswert der Wartezeit
ist dann genau das Reziproke von
eines Poisson-Prozesses auffassen. Man kann
dann keine Aussage mehr über den Zeitpunkt der Sprünge machen, nur über die
Wartezeit auf Sprünge bestimmter Amplitude. Der Erwartungswert der Wartezeit
ist dann genau das Reziproke von 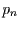 und die Wartezeit ist exponentiell
verteilt. Für die entstehende Zeitreihe gilt dann
und die Wartezeit ist exponentiell
verteilt. Für die entstehende Zeitreihe gilt dann
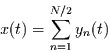 |
(64) |
mit
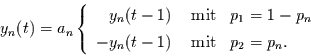 |
(65) |
Die Sprungamplitude 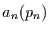 hat die Auftrittswahrscheinlichkeit
hat die Auftrittswahrscheinlichkeit
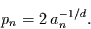 |
(66) |
Dies ist eine hyperbolische Wahrscheinlichkeitsverteilung. Die wesentliche
Information, die über die Zukunft gegeben werden kann, besteht darin, das
kleinere Abweichungen vom momentanen Zustand wahrscheinlicher sind als
große Abweichungen. Bedenkt man, das es sich um einen Prozeß mit langem
Gedächtnis handelt, ist dies nicht viel.
Die physikalische Begründung dieses Modells liegt darin, daß man ein
Potential definieren kann, das zahlreiche Mulden aufweist. Sie repräsentieren
die Nichtlinearität des Systems. Diese Mulden sind unterschiedlich tief,
mit der Bedingung, daß tiefere Mulden weiter voneinander entfernt sind als
weniger tiefe. Die randomisierte Rademacherfunktion der Basisfrequenz 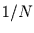 wird also durch die beiden tiefsten Mulden im Potential in einem Abstand von
wird also durch die beiden tiefsten Mulden im Potential in einem Abstand von
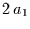 dargestellt. Zu jeder höheren Rademacherfunktion gehören
weniger weit voneinander entfernte aber auch weniger tiefe Potentialmulden.
Wir sehen also, daß eine Zeitreihe mit langem Gedächtnis aus einem stark
zergliederten Potential und Rauschen entstehen kann. Die Existenz von
Zeitreihen mit langem Gedächtnis in einem System kann demnach auch als
Zeiger für ein solches Potential betrachtet werden. Sicher können daraus
Informationen über das System gewonnen werden, diese müssen aber
nicht unbedingt für eine kongrete Vorhersage nützlich sein.
dargestellt. Zu jeder höheren Rademacherfunktion gehören
weniger weit voneinander entfernte aber auch weniger tiefe Potentialmulden.
Wir sehen also, daß eine Zeitreihe mit langem Gedächtnis aus einem stark
zergliederten Potential und Rauschen entstehen kann. Die Existenz von
Zeitreihen mit langem Gedächtnis in einem System kann demnach auch als
Zeiger für ein solches Potential betrachtet werden. Sicher können daraus
Informationen über das System gewonnen werden, diese müssen aber
nicht unbedingt für eine kongrete Vorhersage nützlich sein.




Nächste Seite: Literatur
Aufwärts: Mögliche physikalische Ursachen für
Vorherige Seite: Fehlende räumliche Skala
Inhalt
ich
2000-01-25