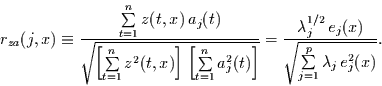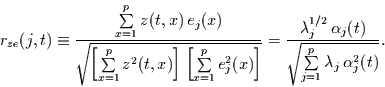

Nächste Seite: Über dieses Dokument ...
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Streumatrix
Man kann zwei Arten von Korrelationen unterscheiden. Einerseits kann man nach
der Korrelation zwischen der Zeitreihe an der Position 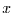 und der PC-Zeitreihe
und der PC-Zeitreihe 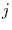 fragen. Diese Korrelation wird hier
fragen. Diese Korrelation wird hier 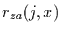 genannt und gibt an, wieviel zeitliche Variation des Ortes
genannt und gibt an, wieviel zeitliche Variation des Ortes 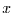 durch die
Zeitreihe des
durch die
Zeitreihe des 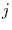 -ten Eigenvektors angegeben ist.
Andererseits kann man nach der räumlichen Korrelation zwischen dem
Ursprungsfeld zur Zeit
-ten Eigenvektors angegeben ist.
Andererseits kann man nach der räumlichen Korrelation zwischen dem
Ursprungsfeld zur Zeit 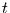 und dem Eigenvektor
und dem Eigenvektor 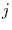 zur Zeit
zur Zeit 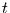 fragen.
Diese Korrelation wird hier als
fragen.
Diese Korrelation wird hier als 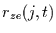 bezeichnet und gibt an, wie
stark der
bezeichnet und gibt an, wie
stark der 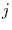 -te Eigenvektor zur Zeit
-te Eigenvektor zur Zeit 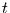 in der beobachteten räumlichen
Struktur vorhanden ist. Für beide Arten der Korrelation können demnach
Karten gemalt werden, von denen eine die Korrelation in Abhängigkeit von
Ort und Eigenvektor ausdrückt, während die andere die Korrelation in
Abhängigkeit von der Zeit und den Eigenvektoren ausdrückt.
Das Produktmoment der Zeitreihe an der Position
in der beobachteten räumlichen
Struktur vorhanden ist. Für beide Arten der Korrelation können demnach
Karten gemalt werden, von denen eine die Korrelation in Abhängigkeit von
Ort und Eigenvektor ausdrückt, während die andere die Korrelation in
Abhängigkeit von der Zeit und den Eigenvektoren ausdrückt.
Das Produktmoment der Zeitreihe an der Position 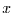 und der PC-Zeitreihe
und der PC-Zeitreihe 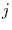 ist gegeben durch
ist gegeben durch
![\begin{displaymath}
\sum\limits_{t=1}^{n} z(t,x) a_{j}(t) =
\sum\limits_{t=1...
..._{k}(t) e_{k}(t)
\right] a_{j}(t) = \lambda_{j} e_{j}(x).
\end{displaymath}](img59.gif) |
(25) |
Damit folgt für den Korrelationskoeffizienten
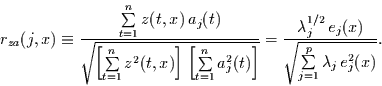 |
(26) |
Analog folgt wegen
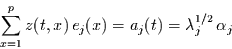 |
(27) |
für
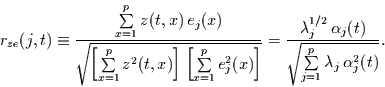 |
(28) |


Nächste Seite: Über dieses Dokument ...
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Streumatrix
ich
2000-01-24
![\begin{displaymath}
\sum\limits_{t=1}^{n} z(t,x) a_{j}(t) =
\sum\limits_{t=1...
..._{k}(t) e_{k}(t)
\right] a_{j}(t) = \lambda_{j} e_{j}(x).
\end{displaymath}](img59.gif)
![\begin{displaymath}
\sum\limits_{t=1}^{n} z(t,x) a_{j}(t) =
\sum\limits_{t=1...
..._{k}(t) e_{k}(t)
\right] a_{j}(t) = \lambda_{j} e_{j}(x).
\end{displaymath}](img59.gif)