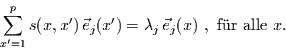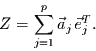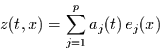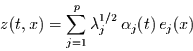

Nächste Seite: Korrelationen
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Nomenklatur
Die Matrix 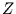 stellt
stellt 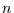 Punkte im
Punkte im 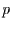 -dimensionalen Raum dar. Jeder Punkt
ist dabei ein Zeitpunkt (man könnte das durchaus auch umgekehrt definieren).
In dem
-dimensionalen Raum dar. Jeder Punkt
ist dabei ein Zeitpunkt (man könnte das durchaus auch umgekehrt definieren).
In dem 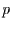 -dimensionalen Raum kann
durch die Basisvektoren
-dimensionalen Raum kann
durch die Basisvektoren
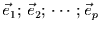 eine beliebige Basis definiert werden.
eine beliebige Basis definiert werden.
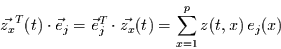 |
(13) |
ist dann die Projektion der durch 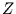 beschriebenen Punktwolke in die
Richtung von
beschriebenen Punktwolke in die
Richtung von 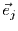 . Als Streuung (Scatter) in Richtung von
. Als Streuung (Scatter) in Richtung von
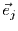 bezeichnet man dann
bezeichnet man dann
![\begin{displaymath}
\Psi(\vec{e}_{j}) \equiv \sum\limits_{t=1}^{n}
\left[\vec...
...\right]
\left[\vec{e}_{j}^{T}\cdot \vec{z_{x}}(t)\right].
\end{displaymath}](img36.gif) |
(14) |
Das ist 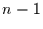 mal die Varianz der Projektion der Punktwolke auf die Achse
mit der Richtung
mal die Varianz der Projektion der Punktwolke auf die Achse
mit der Richtung 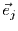 . Gleichung (14) kann leicht umgeformt
werden zu
. Gleichung (14) kann leicht umgeformt
werden zu
![\begin{displaymath}
\Psi(\vec{e}_{j}) = \vec{e}_{j}^{T}
\left[ \sum\limits_{t...
...n}
\vec{z_{x}}(t) \vec{z_{x}}^{T}(t)\right]
\vec{e}_{j}
.\end{displaymath}](img38.gif) |
(15) |
Der Term in den eckigen Klammern in Glg. (15) ist die Streu-
bzw. Scattermatrix. Sie ist 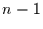 mal die Kovarianzmatrix. Für die Elemente
mal die Kovarianzmatrix. Für die Elemente
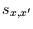 der Scattermatrix gilt:
der Scattermatrix gilt:
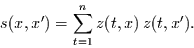 |
(16) |
In Matrixschreibweise bedeutet dies:
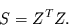 |
(17) |
Die Eigenwerte der Streumatrix sind dann gegeben durch
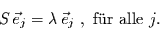 |
(18) |
Das zu lösende Gleichungssystem ist demnach
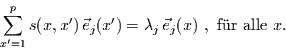 |
(19) |
Mit den Matrixdarstellungen
![$E \equiv [\vec{e}_{1},
\vec{e}_{2}, \cdots ,\vec{e}_{p}]$](img44.gif) und
und
![$L=diag[\lambda_{1},\lambda{2},\cdots,\lambda_{p}]$](img45.gif) und
und
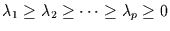 folgt die
Matrixnotation:
folgt die
Matrixnotation:
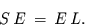 |
(20) |
Nun kann man die Punktwolke 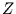 im Eigenvektorsystem
im Eigenvektorsystem 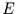 ausdrücken. Dann ist
ausdrücken. Dann ist
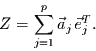 |
(21) |
Dabei sind die Amplitudenvektoren 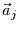 die PC-Zeitreihen
die PC-Zeitreihen
![$\vec{a}_{j}= [a_{j}(1),a_{j}(2),\cdots,a_{j}(n)]^{T}$](img51.gif) .
Damit folgt
.
Damit folgt
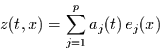 |
(22) |
Die Einführung neuer normalisierter Amplituden
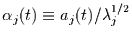 führt zu der
Singular-Value-Decomposition:
führt zu der
Singular-Value-Decomposition:
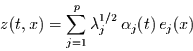 |
(23) |
mit der Matrixschreibweise
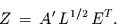 |
(24) |


Nächste Seite: Korrelationen
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Nomenklatur
ich
2000-01-24