

Nächste Seite: Streumatrix
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Ein Beispiel
Gegeben sei die Matrix 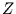 der (
der (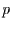 ) zeitlich zentrierten (t-centered)
Zeitreihen der Länge
) zeitlich zentrierten (t-centered)
Zeitreihen der Länge 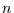 mit den Elementen:
mit den Elementen:
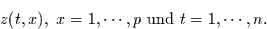 |
(9) |
Die 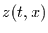 sind skalare Variablen. Ein Schnappschuß der raumzeitlichen
Entwicklung zur Zeit
sind skalare Variablen. Ein Schnappschuß der raumzeitlichen
Entwicklung zur Zeit 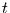 ist dann gegeben durch den Vektor
ist dann gegeben durch den Vektor
![\begin{displaymath}
\vec{z_{x}}(t) =[z(t,1); z(t,2); \cdots ; z(t,p)].
\end{displaymath}](img30.gif) |
(10) |
Die Zeitreihe an einem bestimmten Raumpunkt 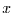 ist gegeben durch
ist gegeben durch
![\begin{displaymath}
\vec{z_{t}}(x) =[z(1,x); z(2,x); \cdots ; z(n,x)].
\end{displaymath}](img31.gif) |
(11) |
Damit ist die Matrix 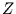 auch darstellbar als Vektor von Vektoren
auch darstellbar als Vektor von Vektoren
![\begin{displaymath}
Z=[\vec{z_{x}}(t=1), \vec{z_{x}}(t=2); \cdots ; \vec{z_...
..._{t}}(x=1), \vec{z_{t}}(x=2); \cdots ; \vec{z_{t}}(x=p)].
\end{displaymath}](img32.gif) |
(12) |
ich
2000-01-24