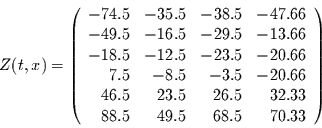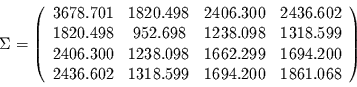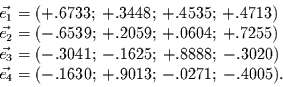

Nächste Seite: Nomenklatur
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Transformationsstrategie
Als Beispiel wird hier eine Hauptkomponententransformation von vier
Temperaturreihen aus dem Mittelmeergebiet durchgeführt. Um Rechenaufwand zu
sparen, werden nur die Monatswerte des ersten Halbjahres 1990 verwendet.
Die Werte sind in Tabelle 1 eingetragen:
Tabelle 1:
Verwendete Datenreihen (Monatsmitteltemperturen in 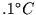 ).
).
| Station |
Januar |
Februar |
März |
April |
Mai |
Juni |
Mittel |
| Athen |
84 |
109 |
140 |
166 |
205 |
247 |
158.5 |
| Gibraltar |
138 |
157 |
161 |
165 |
197 |
223 |
173.5 |
| Luqa |
132 |
141 |
147 |
167 |
197 |
239 |
170.5 |
| Palma |
101 |
135 |
128 |
128 |
181 |
219 |
148.66 |
Der Mittelwertvektor der Punktwolke (die
aus sechs Punkten im vierdimensionalen Raum besteht)
ist gegeben durch
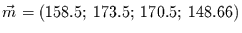 .
Dann folgt für die (schon auf den Mittelwert bezogene) Matrix
.
Dann folgt für die (schon auf den Mittelwert bezogene) Matrix 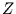 :
:
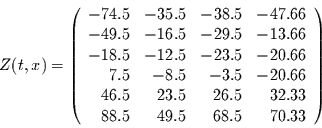 |
(4) |
Als nächstes ist die Kovarianzmatrix zu bestimmen.
Sie ergibt sich zu:
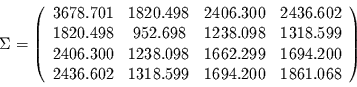 |
(5) |
Für die Korrelationsmatrix 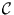 , die die Korrelationskoeffizienten
zwischen je zwei Zeitreihen als Elemente enthält, folgt damit
, die die Korrelationskoeffizienten
zwischen je zwei Zeitreihen als Elemente enthält, folgt damit
 |
(6) |
Die Korrelationen zwischen den Reihen sind sehr hoch. Dies liegt darin, daß
es bei allen Stationen zwischen Januar und Juni wärmer wird.
Zwischen der ersten und der vierten Reihe ist die Korrelation am
geringsten, zwischen der zweiten und der vierten Reihe am höchsten.
Athen und Palma hatten demnach den unterschiedlichsten, Gibraltar und Palma den
ähnlichsten Temperaturverlauf.
Aus Glg. (2) folgen die vier Eigenwerte in absteigender
Reihenfolge:
| 7937.275 |
| 180.048 |
| 37.224 |
| .219 |
Das sind die Varianzen der vier zugeordneten Zeitreihen im gedrehten Raum.
Wie man sieht trägt die vierte Hauptachse kaum noch Varianz bei. Die mit
Abstand meiste Varianz ist in der ersten Hauptachse. Da die neuen Koordinaten
orthogonal sind, kann die Varianz einfach addiert werden. Damit kann man
ausdrücken welcher Anteil der Gesamtvarianz der Punktwolke in welcher
Koordinate liegt.
Die Varianz teilt sich demnach auf die Koordinaten wie folgt auf:
| 97.3330 % |
| 2.2079 % |
| .4565 % |
| .0027 %. |
Die zugeordneten (hier schon normierten) Basisvektoren sind:
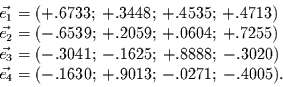 |
(7) |
Man kann sich leicht davon überzeugen, daß diese Vektoren senkrecht
(im Rahmen der Rechengenauigkeit) aufeinanderstehen, indem man das
Skalarprodukt zwischen ihnen bildet. Ebenso einfach sieht man, daß sie
normiert sind, da ihre Länge eins ist.
Es ist nun möglich die Zeitreihen im gedrehten System zu berechnen. Die
Zeitreihe der ersten Hauptkomponente im gedrehten System besteht aus
der Summe der mit den entsprechenden Komponenten des ersten Hauptvektors
multiplizierten Zeitreihen, d.h.
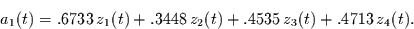 |
(8) |


Nächste Seite: Nomenklatur
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Transformationsstrategie
ich
2000-01-24