

Nächste Seite: Ein Beispiel
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Einleitung
Gegeben sei eine Matrix 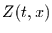 mit
mit 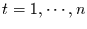 und
und
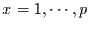 ,
die aus den
,
die aus den 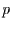 Zeitreihen der Länge
Zeitreihen der Länge 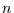 besteht:
besteht:
 |
(1) |
Zunächst wird von jeder Zeitreihe
der Mittelwert dieser Reihe abgezogen. Damit
sind die Spaltensummen und v.a. die Gesamtsumme gleich null und man hat den
Koordinatenursprung in den Schwerpunkt der Punktwolke gesetzt. Im folgenden
werden also nur noch die Abweichungen vom Mittel untersucht.
Die wesentliche Information darüber, wie das System zu drehen ist, steckt in
der Kovarianzmatrix. Die Drehung soll so stattfinden, daß zwischen den
gedrehten Koordinaten keine Kovarianz mehr besteht. Das bedeutet, das die
entstehenden Reihen linear unabhängig werden. Dies ist gleichbedeutend mit
der Forderung der effektivsten Darstellung. Jede neue Koordinate enthält nur
linear unabhängige neue Information. Die Forderung, daß zwischen den neuen
Koordinaten keine Korrelation mehr bestehen soll, läßt sich dadurch
erreichen, daß die Kovarianzmatrix diagonalisiert wird. Die zur
diagonalisierten Kovarianzmatrix gehörenden Eigenvektoren sind eine
Linearkombination der alten Basisvektoren, und drücken damit den
Zusammenhang zwischen den alten und den neuen Zeitreihen aus. Die Eigenwerte
der Kovarianzmatrix (die Diagonalen der diagonalisierten Kovarianzmatrix)
geben die Varianz in dieser (neuen) Koordinatenrichtung an.
Konkret müssen zunächst also die Eigenwerte 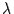 der Kovarianzmatrix
der Kovarianzmatrix 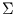 gefunden werden.
Dies geschieht durch Lösen der folgenden Gleichung:
gefunden werden.
Dies geschieht durch Lösen der folgenden Gleichung:
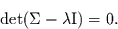 |
(2) |
Dabei stellt I die Einheitsmatrix dar. Da 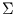 eine
eine 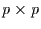 Matrix
ist, existieren
Matrix
ist, existieren 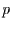 Eigenwerte. Da
Eigenwerte. Da 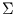 außerdem noch reell und
symmetrisch ist, sind die Eigenwerte alle reell und positiv semidefinit.
Zusätzlich folgt daraus schon, daß die Matrix der Eigenvektoren orthogonal
ist. Hat man die Eigenwerte nach Glg. (2) bestimmt, so kann man
mit
außerdem noch reell und
symmetrisch ist, sind die Eigenwerte alle reell und positiv semidefinit.
Zusätzlich folgt daraus schon, daß die Matrix der Eigenvektoren orthogonal
ist. Hat man die Eigenwerte nach Glg. (2) bestimmt, so kann man
mit
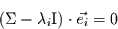 |
(3) |
den 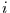 -ten Eigenvektor
-ten Eigenvektor 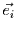 bestimmen.
Die
bestimmen.
Die 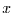 -te Komponente des
-te Komponente des 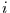 -ten Eigenvektors ist dann
das Gewicht, mit dem die
-ten Eigenvektors ist dann
das Gewicht, mit dem die 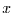 -te Originalzeitreihe in die
-te Originalzeitreihe in die
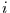 -te Zeitreihe des gedrehten Systems eingeht.
-te Zeitreihe des gedrehten Systems eingeht.


Nächste Seite: Ein Beispiel
Aufwärts: Hauptkomponentenanalyse
Vorherige Seite: Einleitung
ich
2000-01-24

