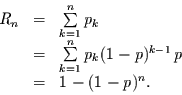


Nächste Seite: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Aufwärts: Der Poisson-Prozeß
Vorherige Seite: Poisson-Prozeß in kontinuierlicher Zeit
Inhalt
Oft betrachtet man diskrete Zeitschritte und berücksichtigt nur, ob
innerhalb eines Zeitschrittes ein Ereignis eingetreten ist, oder nicht. In
diesem Fall, in dem man von 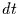 zu
zu 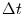 übergeht, verändert sich die
Beschreibung. Betrachtet man nun die Wahrscheinlichkeit
übergeht, verändert sich die
Beschreibung. Betrachtet man nun die Wahrscheinlichkeit 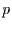 für das Auftreten
eines Ereignisses innerhalb eines Zeitintervalls
für das Auftreten
eines Ereignisses innerhalb eines Zeitintervalls 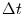 , so kann der
Prozeß als Bernoulli-Experiment beschrieben werden und man hat einen
leichten Zugang zu den Antworten auf verschiedene Fragen.
Wie wahrscheinlich ist es, daß das Ereignis
, so kann der
Prozeß als Bernoulli-Experiment beschrieben werden und man hat einen
leichten Zugang zu den Antworten auf verschiedene Fragen.
Wie wahrscheinlich ist es, daß das Ereignis 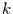 mal in einer Zeitreihe der
Länge
mal in einer Zeitreihe der
Länge 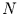 auftritt? Das Ereignis soll also
auftritt? Das Ereignis soll also 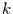 mal auftreten und
mal auftreten und 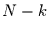 mal
nicht. Dabei soll die Reihenfolge keine Rolle spielen. Demnach folgt für die
Wahrscheinlichkeit für das Auftreten von
mal
nicht. Dabei soll die Reihenfolge keine Rolle spielen. Demnach folgt für die
Wahrscheinlichkeit für das Auftreten von 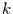 Ereignissen bei
Ereignissen bei 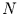 Zeitschritten
Zeitschritten
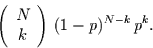 |
(2.14) |
Dies ist die Binomialverteilung, die bekannterweise für kleine 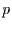 in die
Poissonverteilung übergeht. Damit sieht man, daß wir wegen der Verwendung
von makroskopischen Zeitintervallen
in die
Poissonverteilung übergeht. Damit sieht man, daß wir wegen der Verwendung
von makroskopischen Zeitintervallen 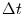 , auf denen wir jetzt den
Prozeß definieren, vom Poisson-Prozeß abgewichen sind.
Wie hoch ist die Wahrscheinlichkeit für das
, auf denen wir jetzt den
Prozeß definieren, vom Poisson-Prozeß abgewichen sind.
Wie hoch ist die Wahrscheinlichkeit für das 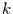 -malige
Hintereinanderauftreten des Ereignisses? Aus dem eben Besprochenen folgt die
Antwort einfach zu
-malige
Hintereinanderauftreten des Ereignisses? Aus dem eben Besprochenen folgt die
Antwort einfach zu 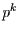 , denn nach wie vor ist die
Eintrittswahrscheinlichkeit eine Konstante.
Wie hoch ist die Wahrscheinlichkeit dafür, daß man
, denn nach wie vor ist die
Eintrittswahrscheinlichkeit eine Konstante.
Wie hoch ist die Wahrscheinlichkeit dafür, daß man 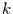 Zeitschritte warten
muß bis das nächste Ereignis eintritt? In diesem Fall darf das Ereignis
Zeitschritte warten
muß bis das nächste Ereignis eintritt? In diesem Fall darf das Ereignis 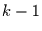 mal nicht eintreten um danach einzutreten. Die Wahrscheinlichkeit, das es in
einem Zeitschritt nicht eintritt, ist gegeben durch
mal nicht eintreten um danach einzutreten. Die Wahrscheinlichkeit, das es in
einem Zeitschritt nicht eintritt, ist gegeben durch 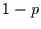 . Demnach folgt für
die Wahrscheinlichkeit, daß erst im
. Demnach folgt für
die Wahrscheinlichkeit, daß erst im 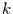 -ten Zeitschritt ein Ereigniss
eintritt
-ten Zeitschritt ein Ereigniss
eintritt
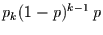 .
Wie lange muß man im Mittel warten, bis das Ereignis eintritt? Die Antwort auf
diese Frage kann nicht leicht aus
.
Wie lange muß man im Mittel warten, bis das Ereignis eintritt? Die Antwort auf
diese Frage kann nicht leicht aus
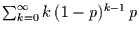 berechnet werden. Wesentlich einfacher geht dies mit Hilfe der erzeugenden
Funktionen, die hier aber nicht zur Verfügung gestellt werden sollen.
Man erhält dann als mittlere Wartezeit
berechnet werden. Wesentlich einfacher geht dies mit Hilfe der erzeugenden
Funktionen, die hier aber nicht zur Verfügung gestellt werden sollen.
Man erhält dann als mittlere Wartezeit 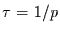 und für deren
Varianz
und für deren
Varianz
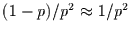 . Die mittlere Wartezeit
ist die Zeit, die in der
Extremwertstatistik Wiederkehrzeit heißt.
Wie hoch ist die Wahrscheinlichkeit
. Die mittlere Wartezeit
ist die Zeit, die in der
Extremwertstatistik Wiederkehrzeit heißt.
Wie hoch ist die Wahrscheinlichkeit 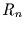 ,
daß in den nächsten
,
daß in den nächsten 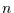 Zeitschritten mindestens
ein Ereignis stattfindet? Die Antwort auf diese Frage ist die Summe über
die Wahrscheinlichkeiten dafür, daß man mindestens
Zeitschritten mindestens
ein Ereignis stattfindet? Die Antwort auf diese Frage ist die Summe über
die Wahrscheinlichkeiten dafür, daß man mindestens 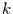 Zeitschritte warten
muß:
Zeitschritte warten
muß:
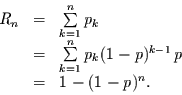 |
(2.15) |
Diese Größe wird in der Extremwertstatistik als Risiko bezeichnet. Sie ist
mit der Wiederkehrzeit wie folgt verknüpft:
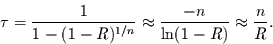 |
(2.16) |
Will man z.B. mit einem Risiko von 10 % in Kauf nehmen, daß ein Ereignis
innerhalb der nächsten einhundert Jahre stattfindet, dann muß die
Wiederkehrzeit des Ereignisses 950 Jahre betragen, falls man es mit einem
stationären Poisson-Prozeß (bzw. einem Bernoulli-Experiment als
dessen zeitdiskrete Form) zu tun hat.



Nächste Seite: Nichtkonstante Ereigniswahrscheinlichkeitsdichten
Aufwärts: Der Poisson-Prozeß
Vorherige Seite: Poisson-Prozeß in kontinuierlicher Zeit
Inhalt
ich
2000-01-24