


Nächste Seite: Betrachtung in diskreten Zeitschritten
Aufwärts: Der Poisson-Prozeß
Vorherige Seite: Der Poisson-Prozeß
Inhalt
Der Poisson-Prozeß ist der einfachste Punktprozeß. Er findet in
kontinuierlicher Zeit statt. Die Eintrittswahrscheinlichkeit eines Ereignisses
im Zeitintervall ![$[t,t+dt]$](img28.gif) ist dabei eine Konstante
ist dabei eine Konstante
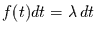 .
Dann ist die Wahrscheinlichkeit dafür, daß ein solches
Ereignis im Zeitintervall
.
Dann ist die Wahrscheinlichkeit dafür, daß ein solches
Ereignis im Zeitintervall
![$[t_{1},t_{1}+dt]$](img23.gif) und im Zeitintervall
und im Zeitintervall
![$[t_{2},t_{2}+dt]$](img24.gif) auftritt, gegeben
durch
auftritt, gegeben
durch
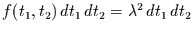 . Die
gemeinsame zweidimensionale Verteilung
faktorisiert demnach in die eindimensionale Verteilung, und diese ist eine
Konstante. Auch alle höherdimensionalen Wahrscheinlichkeitsfunktionen
faktorisieren, so daß gilt
. Die
gemeinsame zweidimensionale Verteilung
faktorisiert demnach in die eindimensionale Verteilung, und diese ist eine
Konstante. Auch alle höherdimensionalen Wahrscheinlichkeitsfunktionen
faktorisieren, so daß gilt
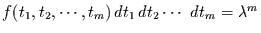 .
Wie hoch ist nun die Wahrscheinlichkeit
.
Wie hoch ist nun die Wahrscheinlichkeit 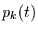 dafür, daß im Zeitraum
dafür, daß im Zeitraum
![$[0,t]$](img38.gif) genau
genau 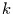 Ereignisse stattfinden? Um diese Frage (und alle damit
zusammenhängenden) lösen zu können, muß die Master-Gleichung für den
Prozeß aufgestellt werden. Die Master-Gleichung ist eine
Differentialgleichung für
Ereignisse stattfinden? Um diese Frage (und alle damit
zusammenhängenden) lösen zu können, muß die Master-Gleichung für den
Prozeß aufgestellt werden. Die Master-Gleichung ist eine
Differentialgleichung für 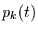 . Auf ihre allgemeine Herleitung muß
hier verzichtet werden, um nicht zu weit vom eigentlichen Ziel
abzurücken. Die Wahrscheinlichkeit zur Zeit
. Auf ihre allgemeine Herleitung muß
hier verzichtet werden, um nicht zu weit vom eigentlichen Ziel
abzurücken. Die Wahrscheinlichkeit zur Zeit 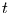 genau
genau 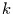 Ereignisse
vorgefunden zu haben, ändert sich durch das Eintreten eines Ereignisses zur
Zeit
Ereignisse
vorgefunden zu haben, ändert sich durch das Eintreten eines Ereignisses zur
Zeit 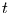 . Falls also zur Zeit
. Falls also zur Zeit 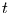
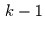 Ereignisse eingetreten waren, so ist
die Wahrscheinlichkeit, daß sich die Anzahl auf
Ereignisse eingetreten waren, so ist
die Wahrscheinlichkeit, daß sich die Anzahl auf 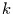 erhöht, gerade
erhöht, gerade
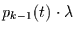 . Andererseits können zur Zeit
. Andererseits können zur Zeit 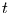 auch schon
auch schon 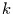 Ereignisse vorliegen. Dann führt das Eintreten eines Ereignisses zur Zeit
Ereignisse vorliegen. Dann führt das Eintreten eines Ereignisses zur Zeit 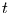 zu einer Veringerung der Wahrscheinlichkeit
zu einer Veringerung der Wahrscheinlichkeit 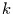 Ereignisse vorzufinden. Für
die Mastergleichung des Poisson-Prozesses folgt daher
Ereignisse vorzufinden. Für
die Mastergleichung des Poisson-Prozesses folgt daher
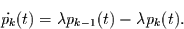 |
(2.1) |
Die Lösung dieser Gleichung ist
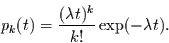 |
(2.2) |
Diese Lösung ist leicht zu verifizieren, indem man sie nach 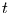 ableitet und
in die linke Seite von Gleichung (2.1) einsetzt.
Spätestens jetzt sollte dem interessierten Leser auffallen, warum der Prozeß
Poisson-Prozeß heißt. Die Anzahl der in einem Zeitintervall der Länge
ableitet und
in die linke Seite von Gleichung (2.1) einsetzt.
Spätestens jetzt sollte dem interessierten Leser auffallen, warum der Prozeß
Poisson-Prozeß heißt. Die Anzahl der in einem Zeitintervall der Länge 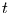 auftretenden Ereignisse ist Poisson-verteilt. Das heißt insbesondere, daß
diese Anzahl für jedes beliebige Intervall nicht von der Vorgeschichte
abhängt. Aus Gleichung (2.2) kann man leicht berechnen, wie
wahrscheinlich es ist, daß über einen Zeitraum der Länge
auftretenden Ereignisse ist Poisson-verteilt. Das heißt insbesondere, daß
diese Anzahl für jedes beliebige Intervall nicht von der Vorgeschichte
abhängt. Aus Gleichung (2.2) kann man leicht berechnen, wie
wahrscheinlich es ist, daß über einen Zeitraum der Länge 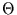 kein
Ereignis eintritt. Diese Wahrscheinlichkeit ist gegeben durch
kein
Ereignis eintritt. Diese Wahrscheinlichkeit ist gegeben durch 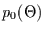 .
Kennt man die Verteilung kann man deren Erwartungswert und Varianz
berechnen. Für den Erwartungswert
.
Kennt man die Verteilung kann man deren Erwartungswert und Varianz
berechnen. Für den Erwartungswert 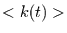 gilt:
gilt:
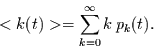 |
(2.3) |
Da der Summand für 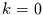 verschwindet, gilt weiter
verschwindet, gilt weiter
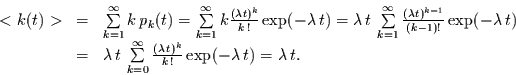 |
(2.4) |
Für die Varianz als zweites zentrales Moment gilt
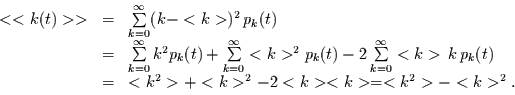 |
(2.5) |
Für das zweite (nichtzentrierte) Moment 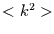 folgt
folgt
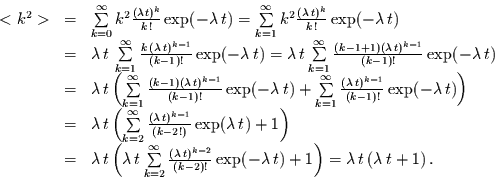 |
(2.6) |
Setzt man diesen Ausdruck in die Gleichung für die Varianz ein, so erhält
man
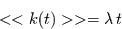 |
(2.7) |
Nun stellt sich die Frage, wie lange man warten muß, bis ein Ereignis
eintritt. Man beginnt also zu einem beliebigen Zeitpunkt 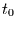 und fragt nach
dem Zeitraum
und fragt nach
dem Zeitraum 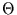 , in dem kein Ereignis auftritt, während zwischen
, in dem kein Ereignis auftritt, während zwischen
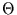 und
und
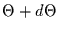 ein Ereignis auftritt. Dieser Zeitraum ist
naturgemäß selbst eine Zufallsvariable, deren Verteilung
ein Ereignis auftritt. Dieser Zeitraum ist
naturgemäß selbst eine Zufallsvariable, deren Verteilung
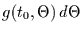 zu bestimmen ist. Dazu sind zwei
Wahrscheinlichkeiten zu betrachten. Einerseits, die Wahrscheinlichkeit, daß
im Intervall
zu bestimmen ist. Dazu sind zwei
Wahrscheinlichkeiten zu betrachten. Einerseits, die Wahrscheinlichkeit, daß
im Intervall
![$[t_{0},t_{0}+\Theta]$](img56.gif) kein Ereignis stattfindet und andererseits
soll dann im Intervall
kein Ereignis stattfindet und andererseits
soll dann im Intervall
![$[t_{0}+\Theta,t_{0}+\Theta+d\Theta]$](img57.gif) mindestens ein
Ereignis stattfinden. Letzteres hat die Wahrscheinlichkeit
mindestens ein
Ereignis stattfinden. Letzteres hat die Wahrscheinlichkeit
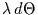 . Ersteres hat die Wahrscheinlichkeit
. Ersteres hat die Wahrscheinlichkeit
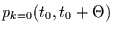 . Demnach ist
. Demnach ist
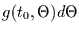 gegeben durch
gegeben durch
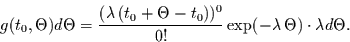 |
(2.8) |
Damit folgt, daß die Wartezeit auf das nächste Ereignis exponentialverteilt
ist, mit
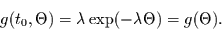 |
(2.9) |
Für den Poisson-Prozeß hängt die Wartezeit auf das nächste Ereignis also
nicht vom Startzeitpunkt ab. Daraus folgt insbesondere auch, daß die
Wartezeit zwischen zwei Ereignissen genau so verteilt ist, wie die Wartezeit
bei beliebigem Startzeitpunkt. Desweiteren sieht man daraus, daß die
Wartezeit nicht von der Wartezeit auf vorherige Ereignisse abhängt. Man beachte auch die Eigenschaft der
Exponentialverteilung, daß kürzeste Wartezeiten die höchste
Wahrscheinlichkeitsdichte haben. Dies mag erschrecken, zumindest aber
verwundern, denn Ereignisse können z.B. Katastrophen sein. Es ist, falls diese
einem Poisson-Prozeß entstammen, dann wahrscheinlicher, daß sie morgen
eintreten als erst übermorgen. Andererseits kann man sich dieses Verhalten am
Beispiel des Würfelns verdeutlichen. Die Wahrscheinlichkeit bei einem Wurf
eine sechs zu würfeln ist ein Sechstel. Die Wahrscheinlichkeit beim ersten
Wurf keine sechs zu würfeln, aber beim zweiten Wurf, ist fünf Sechstel mal
ein Sechstel und damit geringer.
Interessant ist nun der Erwartungswert und
die Varianz der Wartezeit.
Der Erwartungswert (der in der Extremwertstatistik auch Wiederkehrzeit
genannt wird) ist gegeben durch
![\begin{displaymath}
\begin{array}{lll}
<\Theta> & = & \int\limits_{0}^{\infty}...
...right]_{0}^{\infty}\\
& = & \frac{1}{\lambda}
\end{array}
\end{displaymath}](img63.gif) |
(2.10) |
Für den Poissonprozeß ist demnach der Erwartungswert für die Wartezeit auf
ein Ereignis gleich dem Reziproken der Eintrittswahrscheinlichkeit .
Für die Varianz folgt
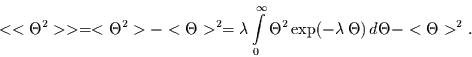 |
(2.11) |
Mit
![\begin{displaymath}
\lambda\,\int\limits_{0}^{\infty} \Theta^{2}\exp(-\lambda\,...
...mbda^{3}}
\right)\right]_{0}^{\infty} =\frac{2}{\lambda^{2}}
\end{displaymath}](img65.gif) |
(2.12) |
folgt daraus
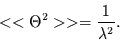 |
(2.13) |



Nächste Seite: Betrachtung in diskreten Zeitschritten
Aufwärts: Der Poisson-Prozeß
Vorherige Seite: Der Poisson-Prozeß
Inhalt
ich
2000-01-24
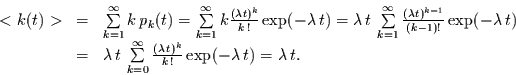
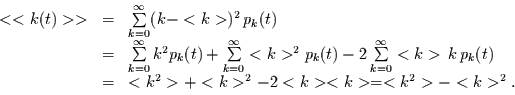
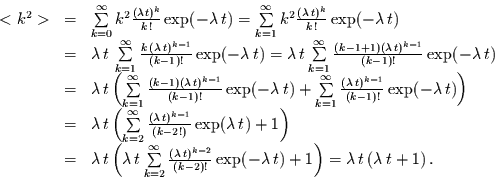
![\begin{displaymath}
\begin{array}{lll}
<\Theta> & = & \int\limits_{0}^{\infty}...
...right]_{0}^{\infty}\\
& = & \frac{1}{\lambda}
\end{array}
\end{displaymath}](img63.gif)
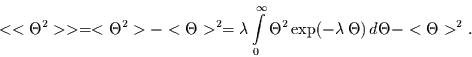
![\begin{displaymath}
\lambda\,\int\limits_{0}^{\infty} \Theta^{2}\exp(-\lambda\,...
...mbda^{3}}
\right)\right]_{0}^{\infty} =\frac{2}{\lambda^{2}}
\end{displaymath}](img65.gif)