

Nächste Seite: Durchführung des Ausreißertests
Aufwärts: Ein Ausreißertest
Vorherige Seite: Anwendbarkeit des Ausreißertests
Zunächst wird von einer Zeitreihe von identisch normalverteilten
unabhängigen Variablen ausgegangen (Gaußsches Rauschen). Diese hat die
Wahrscheinlichkeitsdichtefunktion
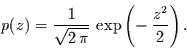 |
(1) |
Für die Wahrscheinlichkeitsfunktion 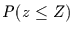 folgt dann
folgt dann
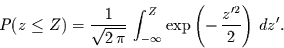 |
(2) |
Für die Wahrscheinlichkeit eine Zahl
zwischen 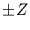 anzutreffen, folgt dann
anzutreffen, folgt dann
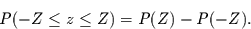 |
(3) |
Da die Wahrscheinlichkeitsdichtefunktion der Normalverteilung
eine gerade Funktion ist, gilt weiter
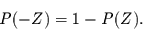 |
(4) |
Daraus folgt sofort:
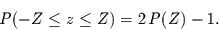 |
(5) |
Aus dem gleichen Grund kann man für 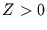 Glg. (2) umformulieren zu
Glg. (2) umformulieren zu
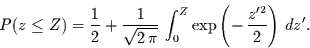 |
(6) |
Dieses Integral ist nicht analytisch lösbar. Jedoch gibt es ein ähnliches
Integral, für das z.B. in den Numerical Recipes Reihen- und
Partialbruchnäherungen angegeben werden.
Dieses ``ähnliche`` Integral
ist die sogenannte Errorfunktion und hat folgende Gestalt:
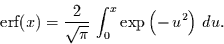 |
(7) |
Um das Integral in Glg. (6) in diese
Form zu bringen wird eine einfache Variablentransformation durchgeführt.
Dazu wird Glg. (6) zunächst umgeschrieben zu
![\begin{displaymath}
P(z\le Z)=\frac{1}{2} + \frac{1}{\sqrt{2\,\pi}}\,\int_{0}^{...
...
\left(-\,\left[\frac{z'}{\sqrt{2}}\right]^{2}\right)\,dz'.
\end{displaymath}](img11.gif) |
(8) |
Transformiert wird nun
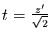 , d.h.
, d.h.
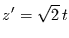 ,
mit der Ableitung
,
mit der Ableitung
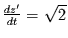 . Damit folgt für
. Damit folgt für 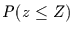
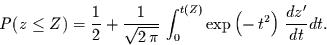 |
(9) |
Setzt man die Ableitung und die transformierte Integralgrenze ein,
so erhält man
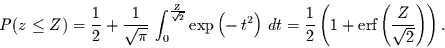 |
(10) |
Aus den Gleichungen (5) und (10) folgt nun
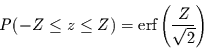 |
(11) |
Dies ist die Wahrscheinlichkeit dafür, durch Zufall aus einer identisch
normalverteilten Variable einen Wert zu ziehen, dessen Betrag kleiner 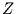 ist.
ist.
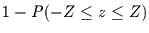 ist dann die Wahrscheinlichkeit durch Zufall einen
mindestens so großen Wert zu ziehen wie
ist dann die Wahrscheinlichkeit durch Zufall einen
mindestens so großen Wert zu ziehen wie 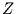 .
Diese Wahrscheinlichkeit gilt für den Fall, daß man einmal zieht.
Die Zeitreihe, die untersucht werden soll, besteht aber aus
.
Diese Wahrscheinlichkeit gilt für den Fall, daß man einmal zieht.
Die Zeitreihe, die untersucht werden soll, besteht aber aus 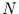 Werten.
Sie stellt damit gemäß den Annahmen eine Realisation dar, bei der
Werten.
Sie stellt damit gemäß den Annahmen eine Realisation dar, bei der
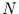 -mal hintereinander (unabhängig) eine solche Zufallszahl gezogen wurde.
Dies wiederum ist ein Bernoulli-Experiment. Die Wahrscheinlichkeit bei
-mal hintereinander (unabhängig) eine solche Zufallszahl gezogen wurde.
Dies wiederum ist ein Bernoulli-Experiment. Die Wahrscheinlichkeit bei
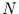 Realisationen
Realisationen 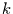 mal einen Wert mit der Eintrittswahrscheinlichkeit
mal einen Wert mit der Eintrittswahrscheinlichkeit
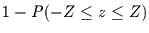 zu erhalten folgt demnach einer Binomialverteilung.
Für Werte von
zu erhalten folgt demnach einer Binomialverteilung.
Für Werte von 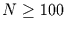 und
und
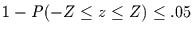 kann diese
Verteilung durch die Poissonverteilung genähert werden.
Somit ist die Wahrscheinlichkeit für das zufällige
kann diese
Verteilung durch die Poissonverteilung genähert werden.
Somit ist die Wahrscheinlichkeit für das zufällige 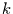 -malige Auftreten
eines solch großen (oder größeren) Wertes gegeben durch
-malige Auftreten
eines solch großen (oder größeren) Wertes gegeben durch
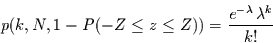 |
(12) |
mit
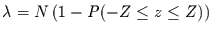 .
Die Wahrscheinlichkeit dafür, daß in einer Zeitreihe der Länge
.
Die Wahrscheinlichkeit dafür, daß in einer Zeitreihe der Länge 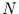 ein solch extremer Wert durch Zufall nicht auftritt ist demnach
ein solch extremer Wert durch Zufall nicht auftritt ist demnach
![\begin{displaymath}
p(k=0,N,1- P(-Z \le z\le Z)) = \exp\left[-N\,\,\mbox{erf}\left(\frac{Z}{\sqrt{2}}\right)\right]
\end{displaymath}](img26.gif) |
(13) |
Damit ist die Wahrscheinlichkeit dafür, daß ein Wert mit dem Abstand
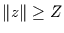 vom Mittelwert der normierten Gaußverteilung in einer Zeitreihe des
Umfangs
vom Mittelwert der normierten Gaußverteilung in einer Zeitreihe des
Umfangs 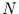 durch Zufall mindestens einmal auftritt, gegeben durch
durch Zufall mindestens einmal auftritt, gegeben durch
![\begin{displaymath}
1-p(k=0,N,1- P(-Z \le z\le Z)) =1 - \exp\left[-N\,\mbox{erf}\left(\frac{Z}{\sqrt{2}}\right)\right].
\end{displaymath}](img28.gif) |
(14) |


Nächste Seite: Durchführung des Ausreißertests
Aufwärts: Ein Ausreißertest
Vorherige Seite: Anwendbarkeit des Ausreißertests
ich
2000-01-24