



Nächste Seite: Statistische Methoden zum Finden
Aufwärts: Rekonstruktionsstrategien
Vorherige Seite: Vorgehensweise
Inhalt
Abschätzung des statistischen Fehlers
Da zur Rekonstruktion optimal angepaßte statistische Modelle verwendet
werden, ist es möglich, aus der Kenntnis der Residuen (des nicht
durch die Anpassung erklärten Anteils) den statistischen Fehler der
Rekonstruktion abzuschätzen.
Als statistisches Modell wird hier ein Modell verstanden, das eine beste
Anpassung zwischen 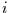 Einflußzeitreihen
Einflußzeitreihen 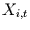 und einer Zielzeitreihe
und einer Zielzeitreihe
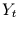 macht. Dieses Modell kann dann dazu verwendet werden, um die
Zielzeitreihe aufgrund vorhergehender Werte der
Einflußzeitreihe zu rekonstruieren. Je nachdem wie gut die
Anpassung ist, wird man einen mehr oder weniger hohen statistischen Fehler
machen. Diesen gilt es abzuschätzen. Der statistische Fehler muß dabei klar
vom systematischen Fehler der Modellanpaßung unterschieden werden.
Letzterer kann als
vernachlässigbar angesehen werden, wenn die Differenz aus aufgrund der
Anpassung erklärtem Anteil an der Zielzeitreihe
macht. Dieses Modell kann dann dazu verwendet werden, um die
Zielzeitreihe aufgrund vorhergehender Werte der
Einflußzeitreihe zu rekonstruieren. Je nachdem wie gut die
Anpassung ist, wird man einen mehr oder weniger hohen statistischen Fehler
machen. Diesen gilt es abzuschätzen. Der statistische Fehler muß dabei klar
vom systematischen Fehler der Modellanpaßung unterschieden werden.
Letzterer kann als
vernachlässigbar angesehen werden, wenn die Differenz aus aufgrund der
Anpassung erklärtem Anteil an der Zielzeitreihe
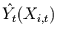 und
der Zielzeitreihe selbst als Rauschen aufgefaßt werden kann. Dann trägt nur
noch dieses statistische Rauschen zum Fehler der
Rekonstruktion bei.
Hier soll nun angegeben werden, wie unter dieser
Vorraussetzung der statistische Fehler der Rekonstruktion
von der erklärten Varianz der Anpassung und der Standardabweichung der
Rekonstruktion abhängt. Dazu wird zunächst die Varianz der Zielzeitreihe
und
der Zielzeitreihe selbst als Rauschen aufgefaßt werden kann. Dann trägt nur
noch dieses statistische Rauschen zum Fehler der
Rekonstruktion bei.
Hier soll nun angegeben werden, wie unter dieser
Vorraussetzung der statistische Fehler der Rekonstruktion
von der erklärten Varianz der Anpassung und der Standardabweichung der
Rekonstruktion abhängt. Dazu wird zunächst die Varianz der Zielzeitreihe
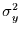 in zwei Anteile aufgespalten:
in zwei Anteile aufgespalten:
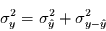 |
(4.1) |
wobei
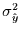 der Anteil der Varianz ist, der durch die
Einflußzeitreihen erklärt wird, während
der Anteil der Varianz ist, der durch die
Einflußzeitreihen erklärt wird, während
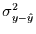 der Anteil
der Varianz von
der Anteil
der Varianz von 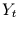 ist, der nicht durch die
ist, der nicht durch die 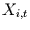 erklärt ist. Teilt
man Gleichung (4.1) durch
erklärt ist. Teilt
man Gleichung (4.1) durch
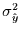 so erhält man
folgenden Ausdruck
so erhält man
folgenden Ausdruck
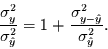 |
(4.2) |
Nun ist der Ausdruck auf der linken Seite von Gleichung (4.2) gleich
dem Reziproken des Bestimmtheitsmaßes 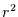 (oft auch erklärte Varianz
genannt, obwohl es keine Varianz ist, sondern ein Varianzanteil). Setzt man
(oft auch erklärte Varianz
genannt, obwohl es keine Varianz ist, sondern ein Varianzanteil). Setzt man
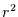 in Gleichung (4.2) ein, stellt nach dem rechten Term auf der
rechten Seite um und zieht die Wurzel, so erhält man
in Gleichung (4.2) ein, stellt nach dem rechten Term auf der
rechten Seite um und zieht die Wurzel, so erhält man
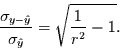 |
(4.3) |
Gleichung (4.3) gibt demnach die Abhängigkeit des Verhältnisses
der Standardabweichung des
nicht erklärten Anteils zu der des erklärten Anteils als Funktion des
Bestimmtheitsmaßes an. Damit ist man in der Lage aus der Standardabweichung
der Vorhersage oder Rekonstruktion auf die Standardabweichung des zugehörigen
statistischen Fehlers zu schließen.
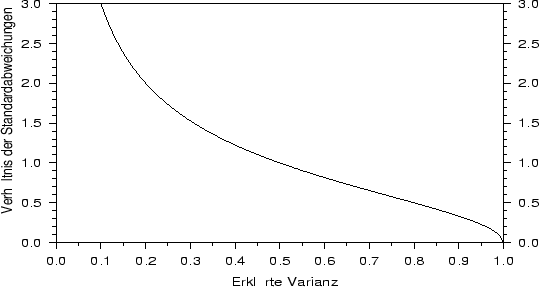
Wie sensibel diese Abhängigkeit insbesondere für nicht sehr große
erklärte Varianzen ist, zeigt Abbildung 4.1. So ist z.B. bei einer
erklärten Varianz von 80 % die Standardabweichung des statistischen
Fehlers noch halb so groß wie die der Rekonstruktion.
Aus der Kenntnis von
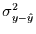 können dann Vertrauensgrenzen für die
Rekonstruktionswerte angegeben werden. Unter der Bedingung, daß der
statistische Fehler normalverteilt ist, folgt:
können dann Vertrauensgrenzen für die
Rekonstruktionswerte angegeben werden. Unter der Bedingung, daß der
statistische Fehler normalverteilt ist, folgt:
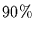
- der wahren Werte liegen weniger als
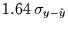 vom Modellwert entfernt,
vom Modellwert entfernt,
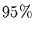
- der wahren Werte liegen weniger als
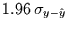 vom
Modellwert entfernt und
vom
Modellwert entfernt und
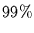
- der wahren Werte liegen weniger als
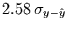 vom Modellwert entfernt.
vom Modellwert entfernt.
Abbildung:
Verhältnis der Standardabweichung
des statistischen Fehlers zur Standardabweichung der Rekonstruktion
in Abhängigkeit von der erklärten Varianz der Anpassung (s. Glg.
(4.3)).
 |




Nächste Seite: Statistische Methoden zum Finden
Aufwärts: Rekonstruktionsstrategien
Vorherige Seite: Vorgehensweise
Inhalt
ich
2000-01-24
