



Nächste Seite: Ergebnisse der Suche nach
Aufwärts: Suche nach globalen Zusammenhängen
Vorherige Seite: Wie stark ist ein
Inhalt
Welcher Art ist ein möglicher stochastischer Zusammenhang?
Nachdem man nun testen kann, ob und wie stark ein Zusammenhang zwischen
zwei Zufallsvariablen ist, stellt sich als nächste Frage, von welcher Art
er ist.
Dazu werden drei mögliche Arten des Zusammenhangs unterschieden:
- linear
- monoton
- nicht monoton.
Falls der Zusammenhang rein linear ist, sollte der
Pearson-Korrelationskoeffizient gleich dem Transinformationskoeffizienten
sein. Theoretisch ist dies möglich, praktisch jedoch extrem
unwahrscheinlich. Nur wenn in der Praxis der Transinformationskoeffizient
signifikant größer ist als der Pearson-Korrelationskoeffizient, kann man
mit einer bestimmten Irrtumswahrscheinlichkeit sagen, daß der Zusammenhang
nicht linear ist. Die Signifikanz kann man über die Konfidenzintervalle
des Korrelationskoeffizienten berechnen. (Die Konfidenzintervalle sollten
mit der Fisher-Transformierten berechnet werden [14].)
Um monotone aber nicht lineare Zusammenhänge zu sehen, haben Spearman und
Kendall Methoden entwickelt [12]. Spearmans Methode basiert darauf,
Ranglistenplätze zu korrelieren (Pearson-Korrelation der Ranglistenplätze).
Das heißt, falls großen Werten in 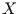 immer auch große Werte in
immer auch große Werte in
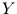 zugeordnet sind, und kleinen Werten in
zugeordnet sind, und kleinen Werten in 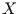 immer auch kleine Werte in
immer auch kleine Werte in
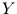 , dann ist der Spearmankoeffizient eins, sonst geringer. Falls größeren
, dann ist der Spearmankoeffizient eins, sonst geringer. Falls größeren
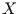 -Werten kleinere
-Werten kleinere 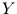 -Werte zugeordnet sind, ist der Koeffizient negativ.
Auch für den Spearman-Koeffizienten
-Werte zugeordnet sind, ist der Koeffizient negativ.
Auch für den Spearman-Koeffizienten 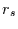 kann die Signifikanz getestet werden.
Und zwar ist die Größe
kann die Signifikanz getestet werden.
Und zwar ist die Größe 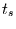 mit
mit
t-verteilt mit 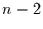 Freiheitsgraden.
Obwohl die Spearman-Korrelation unabhängig von der Verteilung der Variablen
ist, gibt es doch das Problem, daß die hohen Rangplätze in die Korrelation
wesentlich stärker eingehen als die niedrigen. Damit reagiert die
Spearman-Korrelation empfindlich auf Ausreißer. Um dieses Problem zu umgehen,
hat Kendall einen Koeffizienten
Freiheitsgraden.
Obwohl die Spearman-Korrelation unabhängig von der Verteilung der Variablen
ist, gibt es doch das Problem, daß die hohen Rangplätze in die Korrelation
wesentlich stärker eingehen als die niedrigen. Damit reagiert die
Spearman-Korrelation empfindlich auf Ausreißer. Um dieses Problem zu umgehen,
hat Kendall einen Koeffizienten 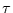 eingeführt. Dieser Koeffizient
berücksichtigt nur die Summe der Vorzeichen des Produkts zwischen
eingeführt. Dieser Koeffizient
berücksichtigt nur die Summe der Vorzeichen des Produkts zwischen
 und
und 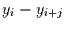 . Es gehen also nur Rangplatzunterschiede
ein, ohne Berücksichtigung deren Größe. Dadurch reagiert Kendall's
. Es gehen also nur Rangplatzunterschiede
ein, ohne Berücksichtigung deren Größe. Dadurch reagiert Kendall's 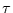 allerdings empfindlich auf Rauschen. Kendall's
allerdings empfindlich auf Rauschen. Kendall's 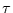 kann zwischen
minus eins und eins normiert werden. Kendall hat auch gezeigt, daß unter der
Annahme keines monotonen Zusammenhangs der Wert
kann zwischen
minus eins und eins normiert werden. Kendall hat auch gezeigt, daß unter der
Annahme keines monotonen Zusammenhangs der Wert 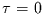 mit der
Standardabweichnung
mit der
Standardabweichnung
zu erwarten ist und daß dann 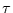 annähernd normalverteilt ist.
Falls die Variablen nur ordinal skaliert sind, ist der Kendall-Koeffizient
dem Spearman-Koeffizient überlegen. Ansonsten neigt er wegen des
Informationsverlustes (als Folge der ausschießlichen Berücksichtigung der
Vorzeichen) dazu, einen Zusammenhang zu unterschätzen.
Falls also aus dem Unabhängigkeitstest folgt, daß
sehr wahrscheinlich ein Zusammenhang vorliegt, dessen Größe man aus dem
Transinformationskoeffizienten bekommt, und alle drei
Korrelationskoeffizienten ununterscheidbar davon sind, handelt es sich um
einen linearen Zusammenhang. Falls der Pearsonkoeffizient signifikant kleiner
ist als der Transinformationskoeffizient, nicht aber der Spearman, bzw.
Kendall-Koeffizient, kann man von einem monotonen Zusammenhang ausgehen.
Sind aber alle Korrelationskoeffizienten kleiner als die
informationstheoretische Kontingenz, folgt daraus, daß ein nicht-linearer und
nicht-monotoner Zusammenhang vorliegt. Dann hilft meiner Meinung nach nur
ein Blick auf das Scatterdiagramm weiter, auf dem man vielleicht die Form
des Zusammenhangs sehen kann.
annähernd normalverteilt ist.
Falls die Variablen nur ordinal skaliert sind, ist der Kendall-Koeffizient
dem Spearman-Koeffizient überlegen. Ansonsten neigt er wegen des
Informationsverlustes (als Folge der ausschießlichen Berücksichtigung der
Vorzeichen) dazu, einen Zusammenhang zu unterschätzen.
Falls also aus dem Unabhängigkeitstest folgt, daß
sehr wahrscheinlich ein Zusammenhang vorliegt, dessen Größe man aus dem
Transinformationskoeffizienten bekommt, und alle drei
Korrelationskoeffizienten ununterscheidbar davon sind, handelt es sich um
einen linearen Zusammenhang. Falls der Pearsonkoeffizient signifikant kleiner
ist als der Transinformationskoeffizient, nicht aber der Spearman, bzw.
Kendall-Koeffizient, kann man von einem monotonen Zusammenhang ausgehen.
Sind aber alle Korrelationskoeffizienten kleiner als die
informationstheoretische Kontingenz, folgt daraus, daß ein nicht-linearer und
nicht-monotoner Zusammenhang vorliegt. Dann hilft meiner Meinung nach nur
ein Blick auf das Scatterdiagramm weiter, auf dem man vielleicht die Form
des Zusammenhangs sehen kann.




Nächste Seite: Ergebnisse der Suche nach
Aufwärts: Suche nach globalen Zusammenhängen
Vorherige Seite: Wie stark ist ein
Inhalt
ich
2000-01-24