



Nächste Seite: Suche nach speziellen Zusammenhängen
Aufwärts: Suche nach globalen Zusammenhängen
Vorherige Seite: Welcher Art ist ein
Inhalt
Ergebnisse der Suche nach globalen Zusammenhängen
Bei der Suche nach globalen Zusammenhängen werden die vier im vorigen
Abschnitt vorgestellten Koeffizienten berechnet, deren Signifikanz und der
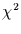 -Unabhängigkeitstest. Da man davon ausgehen kann, daß auch die
klimatischen Bedingungen des Vorjahres einen Einfluß auf das Baumwachstum
haben, werden alle diese Größen auch für die Monatswerte von Niederschlag
und Temperatur des Vorjahres berechnet. Um das Problem der Zufälligkeit
von statistischen Zusammenhängen zu beleuchten werden zusätzlich auch die
klimatischen Monatswerte des Folgejahres mit in Betracht gezogen. Zwischen
den letzteren und dem Baumwachstum sollten keine signifikanten statistischen
Zusammenhänge zu finden sein. Insgesamt werden demnach alle betrachteten
Koeffizienten und deren Signifikanzen für 36 Monatsmitteltemperaturen und
36 monatliche Niederschlagssummen pro Jahrring berechnet. In den Abbildungen
4.2 und 4.3 sind im oberen Teil jeweils die Koeffizienten des
Zusammenhangs zwischen Temperatur und Baumwachstum (Abb. 4.2) und
Niederschlag und Baumwachstum (Abb. 4.3) eingezeichnet.
Man sieht bei den statistischen Zusammenhängen zwischen Temperatur
und Jahrringbreiten (Abb. 4.2)
-Unabhängigkeitstest. Da man davon ausgehen kann, daß auch die
klimatischen Bedingungen des Vorjahres einen Einfluß auf das Baumwachstum
haben, werden alle diese Größen auch für die Monatswerte von Niederschlag
und Temperatur des Vorjahres berechnet. Um das Problem der Zufälligkeit
von statistischen Zusammenhängen zu beleuchten werden zusätzlich auch die
klimatischen Monatswerte des Folgejahres mit in Betracht gezogen. Zwischen
den letzteren und dem Baumwachstum sollten keine signifikanten statistischen
Zusammenhänge zu finden sein. Insgesamt werden demnach alle betrachteten
Koeffizienten und deren Signifikanzen für 36 Monatsmitteltemperaturen und
36 monatliche Niederschlagssummen pro Jahrring berechnet. In den Abbildungen
4.2 und 4.3 sind im oberen Teil jeweils die Koeffizienten des
Zusammenhangs zwischen Temperatur und Baumwachstum (Abb. 4.2) und
Niederschlag und Baumwachstum (Abb. 4.3) eingezeichnet.
Man sieht bei den statistischen Zusammenhängen zwischen Temperatur
und Jahrringbreiten (Abb. 4.2)
- einen nur unwesentlichen Unterschied zwischen den Maßen des monotonen
und linearen Zusammenhangs (d.h. eine monotone Abbildung würde keine besseren
Ergebnisse liefern als eine lineare),
- daß die Transinformationskoeffizienten kaum größer sind als die
Beträge der anderen Koeffizienten (was bedeutet, daß auch ein allgemeiner
nichtinearer Zusammenhang keine besseren Ergebnisse liefern würde als ein
linearer),
- eine deutliche Variabilität des statistischen Zusammenhangs
von Monat zu Monat, wobei die Werte des Vorjahres schwach negativ eingehen,
der Vorwinter positiv und der Sommer des zugeordneten Jahres wieder negativ
(dabei insbesondere der Juni und August),
- auch statistische Zusammenhänge zu den klimatischen Parameter des
Folgejahres zu sehen sind.
Bei den statistischen Zusammenhängen zwischen den monatlichen
Niederschlagssummen und den Jahrringbreiten (Abb. 4.3) erkennt man
- einen nur unwesentlichen Unterschied zwischen den Koeffizienten des
monotonen und linearen Zusammenhangs, aber
- einen deutlich größeren Koeffizienten der Transinformation, was
suggeriert, daß man mit einem nicht-linearen und nicht-monotonen Zusammenhang
deutlich mehr Varianz erklären können wird,
- während der monotone und lineare Zusammenhang für fast alle Monate
um null schwankt, ist er für den Mai des Vorjahres stark negativ und für
den Juli des Wachstumsjahres stark positiv.
Es stellt sich nun die Frage, für welche der statistischen Zusammenhänge
die oben diskutierten Koeffizienten glaubwürdig (in statistischem Sinne) sind.
Dazu wird zu allen Koeffizienten die Signifikanz berechnet. Diese sagt aus,
bei welchem Anteil von Gauß'schen weißen Zufallsreihen der gleichen Länge
kein solch hoher Koeffizient auftritt. Die Signifikanzen der einzelnen
Koeffizienten und die Ergebnisse des 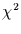 -Unabhängigkeitstests sind
in den unteren Teilen der Abbildungen 4.2 und 4.3 für
Werte größer .9 dargestellt. Bei der Interpretation der Ergebnisse ist
folgendes zu beachten. Ein Wert von .9 bedeutet, daß nur in 10 % der Fälle
ein so hoher Koeffizient durch Zufall auftritt. Da nun aber ein Jahr 12
Monate hat ist es wahrscheinlicher, daß pro untersuchtes Jahr ein Koeffizient
durch Zufall so hoch ist, als das kein Koeffizient dieses 90 %
Signifikanzniveau überschreitet. Deshalb soll nun für die Schwellen
-Unabhängigkeitstests sind
in den unteren Teilen der Abbildungen 4.2 und 4.3 für
Werte größer .9 dargestellt. Bei der Interpretation der Ergebnisse ist
folgendes zu beachten. Ein Wert von .9 bedeutet, daß nur in 10 % der Fälle
ein so hoher Koeffizient durch Zufall auftritt. Da nun aber ein Jahr 12
Monate hat ist es wahrscheinlicher, daß pro untersuchtes Jahr ein Koeffizient
durch Zufall so hoch ist, als das kein Koeffizient dieses 90 %
Signifikanzniveau überschreitet. Deshalb soll nun für die Schwellen
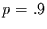 , .95 und .99 berechnet werden, wie wahrscheinlich es ist,
daß
, .95 und .99 berechnet werden, wie wahrscheinlich es ist,
daß 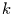 der 12 möglichen Werte durch Zufall über der Schwelle liegen.
Diese Wahrscheinlichkeit folgt der Binomialverteilung (Bernoulli-Experiment)
deren Dichte gegeben ist durch
der 12 möglichen Werte durch Zufall über der Schwelle liegen.
Diese Wahrscheinlichkeit folgt der Binomialverteilung (Bernoulli-Experiment)
deren Dichte gegeben ist durch
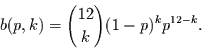 |
(4.11) |
Mit dieser Gleichung kann man berechnen, wieviele Werte 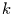 über einer
Schwelle
über einer
Schwelle 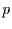 liegen müssen, damit dies ein Ereignis darstellt, daß nur in
liegen müssen, damit dies ein Ereignis darstellt, daß nur in
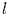 Prozent der Realisationen stattfindet. Die Ergebnisse sind in Tabelle
4.1 angegeben.
Prozent der Realisationen stattfindet. Die Ergebnisse sind in Tabelle
4.1 angegeben.
Tabelle:
Tabelle der Ergebnisse des Tests auf
Überzufälligkeit der
Anzahl der signifikanten Koeffizienten aus den Abbildungen 4.2
und 4.3.
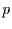 |
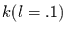 |
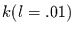 |
| .9 |
3 |
4 |
| .95 |
2 |
3 |
| .99 |
1 |
1 |
Tabelle 4.1 besagt z.B., daß, wenn in einem der drei Jahre (Vorjahr,
Jahr des Wachstums, Folgejahr) vier oder mehr Koeffizienten einer Art
eine Signifikanz größer .9 aufweisen, dies nur mit einer Wahrscheinlichkeit
von 1 % Zufall ist. Benutzt man Tabelle 4.1 Zur Interpretation der
unteren Teile der Abbildungen 4.2 und 4.3, so erkennt man, daß
auch die klimatologische Information des Niederschlags der Folgejahre höchst
signifikant in den Jahrringbreiten zu sehen ist. Andererseits ist die
Temperatur des Vorjahres keinesfalls signifikant in den Jahrringen zu sehen.
Dieses Ergebnis ist außerordentlich befremdend.
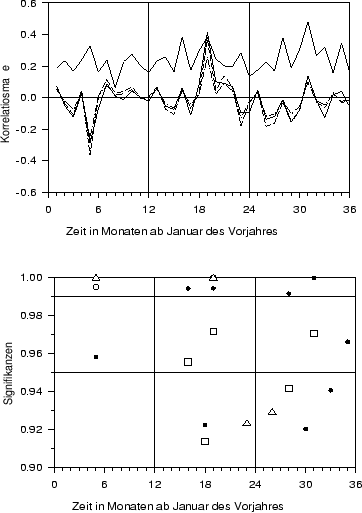
Abbildung:
Oben:
Verschiedene Maße des Zusammenhangs zwischen der
Zeitreihe der Jahrringbreiten von Kiefern in Brandenburg und
Monatsmitteltemperaturen in Potsdam zwischen 1891 und 1991: Transinformation
(dicke durchgezogene Linie), Pearson-Korrelation (dünne durchgezogene Linie),
Spearman-Korrelation (dünne unterbrochene Linie) und Kendall-Korrelation
(Strichpunktlinie).
Unten: Verschiedene Signifikanzmaße: Quadrate 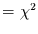 ,
,
 = Signifikanz der Spearman-Korrelation,
= Signifikanz der Spearman-Korrelation,  =
Signifikanz der Pearson-Korrelation und
=
Signifikanz der Pearson-Korrelation und  = Signifikanz der
Transinformation.
= Signifikanz der
Transinformation.
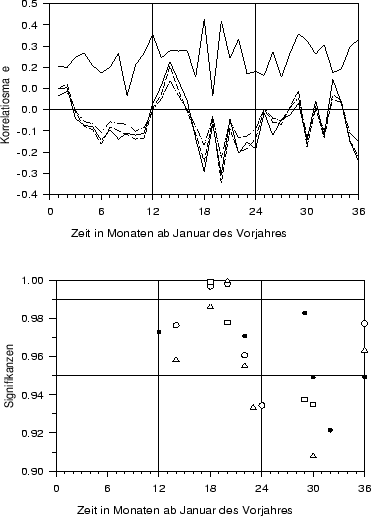 |
Abbildung:
Oben: Verschiedene Maße des Zusammenhangs zwischen der
Zeitreihe der Jahrringbreiten von Kiefern in Brandenburg und monatlicher
Niederschlagssummen in Potsdam zwischen 1891 und 1991: Transinformation
(dicke durchgezogene Linie), Pearson-Korrelation (dünne durchgezogene Linie),
Spearman-Korrelation (dünne unterbrochene Linie) und Kendall-Korrelation
(Strichpunktlinie).
Unten: Verschiedene Signifikanzmaße: Quadrate 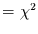 ,
,
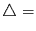 Signifikanz der Spearman-Korrelation,
Signifikanz der Spearman-Korrelation, 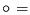 Signifikanz der Pearson-Korrelation und
Signifikanz der Pearson-Korrelation und 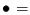 Signifikanz der
Transinformation.
Signifikanz der
Transinformation.
 |




Nächste Seite: Suche nach speziellen Zusammenhängen
Aufwärts: Suche nach globalen Zusammenhängen
Vorherige Seite: Welcher Art ist ein
Inhalt
ich
2000-01-24

