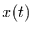Suche nach speziellen Zusammenhängen

Da die Suche nach globalen Zusammenhängen zwischen den klimatologischen Zeitreihen und der Zeitreihe der Jahrringbreiten nicht sehr erfolgreich war, wird nun nach Zusammenhängen zwischen speziellen Komponenten der Zeitreihen gesucht. Dazu wird jede der Zeitreihen entsprechend einer klassischen Zeitreihenanalyse in signifikante orthogonale Anteile zerlegt. Diese können dann jeweils untereinander verglichen werden, so daß ein ähnliches Verhalten unterschiedlicher Reihen bei gleichen Teilkomponenten wie z.B. Extremwerten, Trends oder signifikanten harmonischen Anteilen erkannt werden kann. Dazu werden die Zeitreihen der klimatologischen Parameter in die folgende Summe signifikanter Anteile zerlegt:

$$x(t) = m + t_{r}(t) + s(t) + g(t) + e(t) + h(t) + r(t)$$ (4.12)

mit:

$x(t)$	=	Zeitreihe,
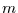$m$	=	Mittelwert der Zeitreihe,
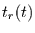$t_{r}(t)$	=	Trendkomponente,
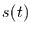$s(t)$	=	saisonale Komponente,
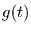$g(t)$	=	glatte Komponente (ohne Trend),
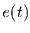$e(t)$	=	seltene (extreme) Ereignisse,
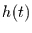$h(t)$	=	harmonische (nichtsaisonale) Komponenten,
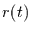$r(t)$	=	Rauschen.

Bei der Zerlegung der Baumringparameterreihe wird natürlich keine signifikante saisonale Komponente gesucht. Die Analyse zeigt, welche dieser Komponenten signifikant in der Zeitreihe zu finden sind, und welche Gestalt sie im Einzelnen haben. In den folgenden Abschnitten sind die Methoden beschrieben, mit deren Hilfe die einzelnen Komponenten in der Zeitreihe detektiert und beschrieben werden, die dann im letzten Abschnitt verglichen werden.