


Nächste Seite: Harmonische Anteile
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Rauschen
Inhalt
Leider gelingt eine Zerlegung, wie sie oben
beschrieben ist, nur selten. Der am wenigsten
kompliziertere Fall ist der, daß
die Verteilung des Residuums fast Gauß-verteilt ist, d.h. hier, daß der
Unterschied zur theoretischen Verteilung von wenigen extremen Werten
herrührt. Diese extremen Werte 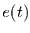 können in der Zeitreihe als seltene
Ereignisse sichtbar sein, ohne welche die Verteilung Gauß-verteilt wäre.
Nachdem die
variable Saisonfigur, Trends und weitere glatte Komponenten eliminiert sind,
können Extremwerte, die nicht zum Rest der Verteilung passen und
somit seltene Ereignisse darstellen, sichtbar werden. Da die Methode der
kleinsten Quadrate, mit welcher die Trendkomponente und die Saisonfigur
angepaßt wurden, sehr sensibel auf extreme Werte reagiert, muß nach der
Eliminierung der Extremwerte erneut die Regression mit den Basisfunktionen
durchgeführt werden.
Findet man Extremwerte, so stellt sich die Frage, woher diese kommen. Es gibt
zwei unterscheidbare Ursachen, die dafür in Frage kommen. Einerseits können
sie seltene zufällige Werte der Beobachtungsgröße selbst sein (und somit
Teil des Rauschens),
andererseits kann ein spezielles Ereignis zu diesen Werten geführt haben
(Ausreißer).
Dies könnten Fehler in der Datenaufnahme und -aufbereitung sein, oder
eine außergewöhnliche klimatologische Situation.
Der im Folgenden vorgestellte Test dient nun dazu, zu berechnen, mit welcher
Wahrscheinlichkeit ein Extremwert ein zufälliges seltenes Ereignis
darstellt, d.h. mit welcher Wahrscheinlichkeit er verträglich mit
der dem Residuum zugrundeliegenden Verteilung ist.
Dazu wird von der Hypothese ausgegangen,
daß die restlichen Werte des Residuums Gauß-verteilt sind. Diese
Hypothese muß natürlich zunächst getestet werden. Falls das Residuum
nicht Gauß-verteilt ist, muß man entweder
können in der Zeitreihe als seltene
Ereignisse sichtbar sein, ohne welche die Verteilung Gauß-verteilt wäre.
Nachdem die
variable Saisonfigur, Trends und weitere glatte Komponenten eliminiert sind,
können Extremwerte, die nicht zum Rest der Verteilung passen und
somit seltene Ereignisse darstellen, sichtbar werden. Da die Methode der
kleinsten Quadrate, mit welcher die Trendkomponente und die Saisonfigur
angepaßt wurden, sehr sensibel auf extreme Werte reagiert, muß nach der
Eliminierung der Extremwerte erneut die Regression mit den Basisfunktionen
durchgeführt werden.
Findet man Extremwerte, so stellt sich die Frage, woher diese kommen. Es gibt
zwei unterscheidbare Ursachen, die dafür in Frage kommen. Einerseits können
sie seltene zufällige Werte der Beobachtungsgröße selbst sein (und somit
Teil des Rauschens),
andererseits kann ein spezielles Ereignis zu diesen Werten geführt haben
(Ausreißer).
Dies könnten Fehler in der Datenaufnahme und -aufbereitung sein, oder
eine außergewöhnliche klimatologische Situation.
Der im Folgenden vorgestellte Test dient nun dazu, zu berechnen, mit welcher
Wahrscheinlichkeit ein Extremwert ein zufälliges seltenes Ereignis
darstellt, d.h. mit welcher Wahrscheinlichkeit er verträglich mit
der dem Residuum zugrundeliegenden Verteilung ist.
Dazu wird von der Hypothese ausgegangen,
daß die restlichen Werte des Residuums Gauß-verteilt sind. Diese
Hypothese muß natürlich zunächst getestet werden. Falls das Residuum
nicht Gauß-verteilt ist, muß man entweder
- eine andere theoretische Verteilung anpassen
(und die Teststrategie erneut lösen), oder
- das Residuum in eine Gauß-verteilte Reihe transformieren.
Hier wird von einem Residuum als einer Zeitreihe von identisch
normalverteilten
unabhängigen Variablen ausgegangen (Gaußsches Rauschen). Diese hat die
Wahrscheinlichkeitsdichtefunktion
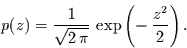 |
(4.17) |
Für die Wahrscheinlichkeitsfunktion 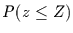 folgt dann
folgt dann
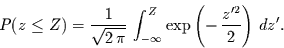 |
(4.18) |
Für die Wahrscheinlichkeit eine Zahl
zwischen 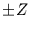 anzutreffen, folgt dann
anzutreffen, folgt dann
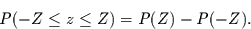 |
(4.19) |
Da die Wahrscheinlichkeitsdichtefunktion der Normalverteilung
eine gerade Funktion ist, gilt weiter
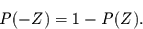 |
(4.20) |
Daraus folgt sofort:
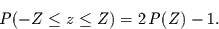 |
(4.21) |
Aus dem gleichen Grund kann man für 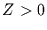 Glg. (4.18) umformulieren zu
Glg. (4.18) umformulieren zu
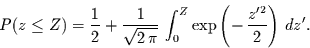 |
(4.22) |
Dieses Integral ist nicht analytisch lösbar. Jedoch gibt es ein ähnliches
Integral, für das z.B. in den Numerical Recipes [12]
Reihen- und Partialbruchnäherungen angegeben werden.
Dieses ``ähnliche`` Integral
ist die sogenannte Errorfunktion und hat folgende Gestalt:
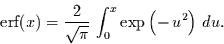 |
(4.23) |
Um das Integral in Glg. (4.22) in diese
Form zu bringen, wird eine einfache Variablentransformation durchgeführt.
Dazu wird Glg. (4.22) zunächst umgeschrieben zu
![\begin{displaymath}
P(z\le Z)=\frac{1}{2} + \frac{1}{\sqrt{2\,\pi}}\,\int_{0}^{...
...
\left(-\,\left[\frac{z'}{\sqrt{2}}\right]^{2}\right)\,dz'.
\end{displaymath}](img146.gif) |
(4.24) |
Transformiert wird nun
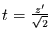 , d.h.
, d.h.
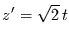 ,
mit der Ableitung
,
mit der Ableitung
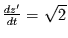 . Damit folgt für
. Damit folgt für 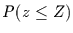
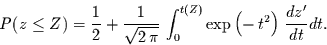 |
(4.25) |
Setzt man die Ableitung und die transformierte Integralgrenze ein,
so erhält man
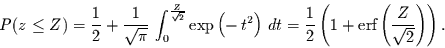 |
(4.26) |
Aus den Gleichungen (4.21) und (4.26) folgt nun
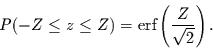 |
(4.27) |
Dies ist die Wahrscheinlichkeit dafür, durch Zufall aus einer identisch
normalverteilten Variable einen Wert zu ziehen, dessen Betrag kleiner 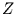 ist.
ist.
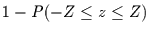 ist dann die Wahrscheinlichkeit durch Zufall einen
mindestens so großen Wert zu ziehen wie
ist dann die Wahrscheinlichkeit durch Zufall einen
mindestens so großen Wert zu ziehen wie 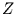 .
Diese Wahrscheinlichkeit gilt für den Fall, daß man einmal zieht.
Die Zeitreihe, die untersucht werden soll, besteht aber aus
.
Diese Wahrscheinlichkeit gilt für den Fall, daß man einmal zieht.
Die Zeitreihe, die untersucht werden soll, besteht aber aus 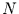 Werten.
Sie stellt damit gemäß den Annahmen eine Realisation dar, bei der
Werten.
Sie stellt damit gemäß den Annahmen eine Realisation dar, bei der
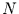 -mal hintereinander (unabhängig) eine solche Zufallszahl gezogen wurde.
Dies wiederum ist ein Bernoulli-Experiment. Die Wahrscheinlichkeit, bei
-mal hintereinander (unabhängig) eine solche Zufallszahl gezogen wurde.
Dies wiederum ist ein Bernoulli-Experiment. Die Wahrscheinlichkeit, bei
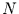 Realisationen
Realisationen 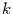 mal einen Wert mit der Eintrittswahrscheinlichkeit
mal einen Wert mit der Eintrittswahrscheinlichkeit
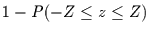 zu erhalten, folgt demnach einer Binomialverteilung.
Für Werte von
zu erhalten, folgt demnach einer Binomialverteilung.
Für Werte von 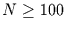 und
und
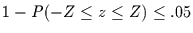 kann diese
Verteilung durch die Poissonverteilung genähert werden.
Somit ist die Wahrscheinlichkeit für das zufällige
kann diese
Verteilung durch die Poissonverteilung genähert werden.
Somit ist die Wahrscheinlichkeit für das zufällige 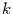 -malige Auftreten
eines solch großen (oder größeren) Wertes gegeben durch
-malige Auftreten
eines solch großen (oder größeren) Wertes gegeben durch
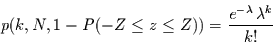 |
(4.28) |
mit
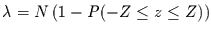 .
Die Wahrscheinlichkeit dafür, daß in einer Zeitreihe der Länge
.
Die Wahrscheinlichkeit dafür, daß in einer Zeitreihe der Länge 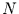 ein solch extremer Wert durch Zufall nicht auftritt ist demnach
ein solch extremer Wert durch Zufall nicht auftritt ist demnach
![\begin{displaymath}
p(k=0,N,1- P(-Z \le z\le Z)) = \exp\left[-N\,\,\mbox{erf}\left(\frac{Z}{\sqrt{2}}\right)\right]
\end{displaymath}](img160.gif) |
(4.29) |
Damit ist die Wahrscheinlichkeit dafür, daß ein Wert mit dem Abstand
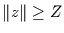 vom Mittelwert der normierten Gaußverteilung in einer Zeitreihe des
Umfangs
vom Mittelwert der normierten Gaußverteilung in einer Zeitreihe des
Umfangs 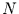 durch Zufall mindestens einmal auftritt, gegeben durch
durch Zufall mindestens einmal auftritt, gegeben durch
![\begin{displaymath}
1-p(k=0,N,1- P(-Z \le z\le Z)) =1 - \exp\left[-N\,\mbox{erf}\left(\frac{Z}{\sqrt{2}}\right)\right].
\end{displaymath}](img162.gif) |
(4.30) |
Bei der Durchführung des Tests wird wie folgt vorgegangen:
Zunächst wird der am weitesten vom Mittelwert entfernte
Wert der Verteilung gesucht und als möglicher Ausreißer ins Auge gefaßt.
Aus den restlichen Werten werden Mittelwert und
Standardabweichung der zugrundeliegenden Verteilung geschätzt. Mit Hilfe
des Kolmogoroff-Smirnoff-Tests wird getestet, ob die Verteilung der
restlichen Werte signifikant von der Gaußverteilung abweicht. Nur wenn dies
nicht der Fall ist, darf der Test weiter durchgeführt werden. Im nächsten
Schritt wird der normierte Abstand des möglichen Ausreißers vom Mittelwert
der Verteilung der restlichen Werte berechnet. Daraufhin kann die
Wahrscheinlichkeit dafür berechnet werden, daß ein Wert, der so weit oder
weiter vom Mittelwert der Verteilung entfernt liegt, durch
Zufall als eine Realisation der Verteilung auftritt (Gleichung (4.27)).
Die Zeitreihe mit
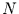 Werten stellt dann ein Bernoulli-Experiment mit
Werten stellt dann ein Bernoulli-Experiment mit 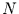 Realisationen dar. Im
letzten Schritt braucht man nun nur noch zu testen, wie wahrscheinlich kein
solch großer Wert in einer Zeitreihe der gegebenen Länge
auftritt (Gleichung (4.29)).
Treten in einer Reihe mehrere seltene Ereignisse auf, so können sie durch
sukzessive Anwendung des Tests gefunden werden (man beachte, daß dann erst
nach Abzug aller Ausreißer die Gaußverteilung erkannt werden muß). In
diesem Fall können folgende Fragen beantwortet werden:
Realisationen dar. Im
letzten Schritt braucht man nun nur noch zu testen, wie wahrscheinlich kein
solch großer Wert in einer Zeitreihe der gegebenen Länge
auftritt (Gleichung (4.29)).
Treten in einer Reihe mehrere seltene Ereignisse auf, so können sie durch
sukzessive Anwendung des Tests gefunden werden (man beachte, daß dann erst
nach Abzug aller Ausreißer die Gaußverteilung erkannt werden muß). In
diesem Fall können folgende Fragen beantwortet werden:
- Treten die seltenen Ereignisse insbesondere in bestimmten Jahreszeiten
auf?
- Handelt es sich um hauptsächlich positive oder negative Extrema?
- Können sie durch einen Extremwertprozeß beschrieben werden?



Nächste Seite: Harmonische Anteile
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Rauschen
Inhalt
ich
2000-01-24