



Nächste Seite: Seltene Ereignisse
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Glatte (tieffrequente) Komponente
Inhalt
Wenn außer dem Trend, der Saisonkomponente und der glatten Komponente keine
weiteren Strukturen in der Zeitreihe vorhanden sind, so muß der nicht durch
diese Komponenten beschriebene Anteil der Zeitreihe durch ein Zufallsrauschen
beschreibbar sein. Dies wird im nächsten Schritt getestet. Dazu wird
zunächst das Residuum
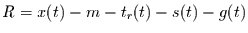 auf seine
Verteilung hin untersucht. Läßt sich die Verteilung nicht von einer
Gauß-Verteilung unterscheiden, so bedeutet das nach dem zentralen
Grenzwertsatz, daß dieses Residuum als Summe vieler im einzelnen
unbedeutender Einflüsse betrachtet werden darf [3].
Getestet wird dies mit dem Kolmogoroff-Smirnoff-Test [12].
Ist das Residuum zusätzlich noch mittelwert-, varianz-
und autokovarianzstationär, so kann es als Realisation eines stochastischen
Prozesses aufgefaßt werden [4]. Die Stationarität des
Residuums wird getestet, indem die Zeitreihe in zwei Intervalle eingeteilt
wird und von jedem Intervall Mittelwert, Standardabweichung und
Autokorrelationsfuntion miteinander verglichen werden. Für die Mittelwerte
wird hierzu ein t-Test verwendet, für die Standardabweichungen ein F-Test
[14]. Zum Test der Autokovarianzstationarität
wird die Autokorrelationsfunktion der ersten und zweiten Hälfte des
Residuums geschätzt und Fisher-Transformiert [14].
Dadurch kann davon ausgegangen werden, daß für jede Zeitverschiebung die
Differenz zwischen dem Autokorrelationskoeffizienten der ersten und der
zweiten Hälfte Gauß-verteilt ist. Damit ist diese Differenz leicht auf
Überzufälligkeit zu testen.
Sind für eine
Residuenreihe die Stationaritätsannahmen erfüllt und ist ihre Verteilung
nicht von einer Gauß-Verteilung zu unterscheiden, so kann weiterhin deren
Autokorrelationsfunktion und partielle Autokorrelationsfunktion untersucht
werden. Damit ist ein linearer stochastischer Prozeß an das Residuum
anpaßbar und die Zeitreihe ist vollständig beschrieben. Zusätzlich kann
auch die Spearman-Autokorrelationsfunktion [12]
und die Autoinformationsfunktion [18] berechnet werden, die
Aufschluß darüber geben, um wieviel besser das Residuum durch eine streng
monotone Abbildung eines linearen Prozesses (Spearman-Koeffizient) oder einen
nichtlinearen stochastischen Prozeß beschreibbar ist (Autoinformation).
auf seine
Verteilung hin untersucht. Läßt sich die Verteilung nicht von einer
Gauß-Verteilung unterscheiden, so bedeutet das nach dem zentralen
Grenzwertsatz, daß dieses Residuum als Summe vieler im einzelnen
unbedeutender Einflüsse betrachtet werden darf [3].
Getestet wird dies mit dem Kolmogoroff-Smirnoff-Test [12].
Ist das Residuum zusätzlich noch mittelwert-, varianz-
und autokovarianzstationär, so kann es als Realisation eines stochastischen
Prozesses aufgefaßt werden [4]. Die Stationarität des
Residuums wird getestet, indem die Zeitreihe in zwei Intervalle eingeteilt
wird und von jedem Intervall Mittelwert, Standardabweichung und
Autokorrelationsfuntion miteinander verglichen werden. Für die Mittelwerte
wird hierzu ein t-Test verwendet, für die Standardabweichungen ein F-Test
[14]. Zum Test der Autokovarianzstationarität
wird die Autokorrelationsfunktion der ersten und zweiten Hälfte des
Residuums geschätzt und Fisher-Transformiert [14].
Dadurch kann davon ausgegangen werden, daß für jede Zeitverschiebung die
Differenz zwischen dem Autokorrelationskoeffizienten der ersten und der
zweiten Hälfte Gauß-verteilt ist. Damit ist diese Differenz leicht auf
Überzufälligkeit zu testen.
Sind für eine
Residuenreihe die Stationaritätsannahmen erfüllt und ist ihre Verteilung
nicht von einer Gauß-Verteilung zu unterscheiden, so kann weiterhin deren
Autokorrelationsfunktion und partielle Autokorrelationsfunktion untersucht
werden. Damit ist ein linearer stochastischer Prozeß an das Residuum
anpaßbar und die Zeitreihe ist vollständig beschrieben. Zusätzlich kann
auch die Spearman-Autokorrelationsfunktion [12]
und die Autoinformationsfunktion [18] berechnet werden, die
Aufschluß darüber geben, um wieviel besser das Residuum durch eine streng
monotone Abbildung eines linearen Prozesses (Spearman-Koeffizient) oder einen
nichtlinearen stochastischen Prozeß beschreibbar ist (Autoinformation).




Nächste Seite: Seltene Ereignisse
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Glatte (tieffrequente) Komponente
Inhalt
ich
2000-01-24