Nächste Seite: Rauschen
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Saisonale Komponente
Inhalt
Um die glatte tieffrequente Komponente der Zeitreihen zu extrahieren, werden
polynomiale Ansätze bis zur fünften Ordnung mit den Residuen der Zeitreihen
(multipel) korreliert, d.h. Ansätze der Form
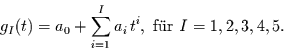 |
(4.16) |
Dabei wird das Polynom der höchsten Ordnung 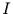 verwendet, daß noch
signifikant mehr Varianz erklärt, als die Polynome mit einer Ordnung kleiner
verwendet, daß noch
signifikant mehr Varianz erklärt, als die Polynome mit einer Ordnung kleiner
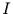 . Dieser Anteil wird mittels einer multiplen Regression aus der Reihe
eliminiert und getrennt betrachtet. Die so eliminierte glatte Komponente kann
bis zu vier Extremwerte (signifikant wärmere und kältere bzw.
niederschlagsreichere und niederschlagsärmere Zeiten bei den klimatologischen
Parametern und Zeiten mit signifikant besserem und schlechterem Baumwachstum
bei den Jahrringreihen) und drei Wendepunkte aufweisen.
Somit erhält man eine Beschreibung der signifikanten glatten Komponente.
Durch starkes Tiefpaßfiltern wäre zwar auch eine glatte Komponente sichtbar
geworden, jedoch hätten keinerlei Aussagen über deren signifikanten Beitrag
zur Varianz der Zeitreihe getroffen werden können. Da für die glatte
Komponente ein polynomialer Ansatz bis zur fünften Ordnung verwendet wurde,
beschreibt sie den niederfrequenten Anteil der Reihe bis zur Wellenzahl 2.
Dieser hätte mit einer harmonischen Analyse nur schlecht
erfaßt werden können, da bei der harmonischen Analyse nach harmonischen
Anteilen mit vorgegebenen festen Perioden (Fourier-Stützstellen) gesucht
wird. Im Gegensatz dazu findet die Anpassung des Polynoms aber auch deutlich
nichtharmonische niederfrequente Schwankungen.
. Dieser Anteil wird mittels einer multiplen Regression aus der Reihe
eliminiert und getrennt betrachtet. Die so eliminierte glatte Komponente kann
bis zu vier Extremwerte (signifikant wärmere und kältere bzw.
niederschlagsreichere und niederschlagsärmere Zeiten bei den klimatologischen
Parametern und Zeiten mit signifikant besserem und schlechterem Baumwachstum
bei den Jahrringreihen) und drei Wendepunkte aufweisen.
Somit erhält man eine Beschreibung der signifikanten glatten Komponente.
Durch starkes Tiefpaßfiltern wäre zwar auch eine glatte Komponente sichtbar
geworden, jedoch hätten keinerlei Aussagen über deren signifikanten Beitrag
zur Varianz der Zeitreihe getroffen werden können. Da für die glatte
Komponente ein polynomialer Ansatz bis zur fünften Ordnung verwendet wurde,
beschreibt sie den niederfrequenten Anteil der Reihe bis zur Wellenzahl 2.
Dieser hätte mit einer harmonischen Analyse nur schlecht
erfaßt werden können, da bei der harmonischen Analyse nach harmonischen
Anteilen mit vorgegebenen festen Perioden (Fourier-Stützstellen) gesucht
wird. Im Gegensatz dazu findet die Anpassung des Polynoms aber auch deutlich
nichtharmonische niederfrequente Schwankungen.




Nächste Seite: Rauschen
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Saisonale Komponente
Inhalt
ich
2000-01-24