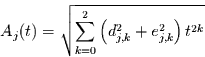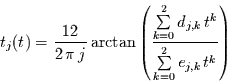Nächste Seite: Glatte (tieffrequente) Komponente
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Trendkomponente
Inhalt
Die saisonale Komponente besteht aus Schwingungen mit den Wellenzahlen
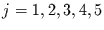 und
und 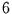 pro Jahr. Damit läßt sich der mittlere Jahresgang der
Monatswerte exakt wiedergeben. Hier wird ein Ansatz gewählt, der nur
signifikante Beiträge selektiert, und es somit erlaubt den signifikanten
Teil des mittleren Jahresgangs anzugeben. Nun muß der
Jahresgang keineswegs starr sein, sondern kann Fluktuationen oder langsamen
systematischen (glatten) Änderungen unterliegen. Um glatte Änderungen im
Jahresgang erfassen zu können, wird zugelassen, daß die Amplitude jeder
im Jahresgang enthaltenen Schwingung sich linear und
quadratisch im Laufe der Zeit ändern kann, d.h. für jede der sechs
Wellenzahlen
pro Jahr. Damit läßt sich der mittlere Jahresgang der
Monatswerte exakt wiedergeben. Hier wird ein Ansatz gewählt, der nur
signifikante Beiträge selektiert, und es somit erlaubt den signifikanten
Teil des mittleren Jahresgangs anzugeben. Nun muß der
Jahresgang keineswegs starr sein, sondern kann Fluktuationen oder langsamen
systematischen (glatten) Änderungen unterliegen. Um glatte Änderungen im
Jahresgang erfassen zu können, wird zugelassen, daß die Amplitude jeder
im Jahresgang enthaltenen Schwingung sich linear und
quadratisch im Laufe der Zeit ändern kann, d.h. für jede der sechs
Wellenzahlen 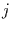 wird für die Amplituden der harmonischen Anteile ein
quadratisches Polynom angesetzt. Damit folgt für die saisonale Komponente
und deren glatte zeitliche Änderung ein Ansatz mit folgenden 18
Termen:
wird für die Amplituden der harmonischen Anteile ein
quadratisches Polynom angesetzt. Damit folgt für die saisonale Komponente
und deren glatte zeitliche Änderung ein Ansatz mit folgenden 18
Termen:
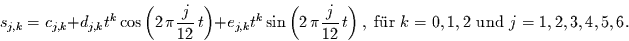 |
(4.14) |
Dieser Ansatz berücksichtigt die starren Anteile (k=0), die sich linear
mit der Zeit ändernden Anteile (k=1) und die sich stärker als linear mit
der Zeit ändernden Anteile (k=2) für alle sechs Wellenzahlen 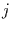 . So
können zusätzlich zum signifikanten Jahresgang auch signifikante lineare
und progressiv sowie degressiv steigende bzw. fallende Änderungen in der
Amplitude und Phase des Jahresgangs erkannt werden. Die zu einer Wellenzahl
gehörenden Komponenten können zusammengefaßt werden zu
. So
können zusätzlich zum signifikanten Jahresgang auch signifikante lineare
und progressiv sowie degressiv steigende bzw. fallende Änderungen in der
Amplitude und Phase des Jahresgangs erkannt werden. Die zu einer Wellenzahl
gehörenden Komponenten können zusammengefaßt werden zu
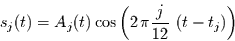 |
(4.15) |
mit der Amplitudenfunktion
,
für alle signifikanten 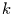 und der Phasenverschiebung
und der Phasenverschiebung
,
für alle signifikanten 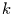 .
Falls zu einer bestimmten Wellenzahl
.
Falls zu einer bestimmten Wellenzahl 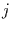 nur ein signifikantes
nur ein signifikantes 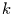 gefunden
wird, bedeutet dies, daß sich die
Phasenlage nicht ändert, während sich die Amplitude gemäß
gefunden
wird, bedeutet dies, daß sich die
Phasenlage nicht ändert, während sich die Amplitude gemäß 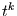 ändert. Damit läßt sich schon allein aus der Kenntnis der signifikanten
Anteile eine Aussage über strukturierte Veränderungen in der Amplitude und
Phasenlage des Jahresgangs treffen. Der signifikante Jahresgang ist dann
darstellbar als Summe über alle signifikanten
ändert. Damit läßt sich schon allein aus der Kenntnis der signifikanten
Anteile eine Aussage über strukturierte Veränderungen in der Amplitude und
Phasenlage des Jahresgangs treffen. Der signifikante Jahresgang ist dann
darstellbar als Summe über alle signifikanten 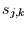 .
Um signifikante Trendkomponenten und starre bzw. glatt veränderliche
Saisonfiguren zu finden, wird nach signifikanten Zusammenhängen der zu
untersuchenden Zeitreihen und den 23 orthogonalen Basisfunktionen (den
fünf Trend- und den 18 Saisonfiguren) gesucht. Der signifikanteste gefundene
Zusammenhang (zu erkennen am höchsten univariaten Korrelationskoeffizienten)
wird dann aus der Reihe eliminiert und gilt als erklärt. Danach wird
erneut nach signifikanten Zusammenhängen des nicht erklärten Anteils mit
diesen Basisfunktionen gesucht. Das Verfahren zieht somit rekursiv immer die
am signifikantesten erklärbaren Anteile ab, bis keine signifikante
Korrelation zu einer der Basisfunktionen mehr besteht. Nach diesem
Arbeitsschritt können folgende Fragen beantwortet werden:
.
Um signifikante Trendkomponenten und starre bzw. glatt veränderliche
Saisonfiguren zu finden, wird nach signifikanten Zusammenhängen der zu
untersuchenden Zeitreihen und den 23 orthogonalen Basisfunktionen (den
fünf Trend- und den 18 Saisonfiguren) gesucht. Der signifikanteste gefundene
Zusammenhang (zu erkennen am höchsten univariaten Korrelationskoeffizienten)
wird dann aus der Reihe eliminiert und gilt als erklärt. Danach wird
erneut nach signifikanten Zusammenhängen des nicht erklärten Anteils mit
diesen Basisfunktionen gesucht. Das Verfahren zieht somit rekursiv immer die
am signifikantesten erklärbaren Anteile ab, bis keine signifikante
Korrelation zu einer der Basisfunktionen mehr besteht. Nach diesem
Arbeitsschritt können folgende Fragen beantwortet werden:
- Gibt es eine signifikante saisonale Komponente und einen signifikanten
Trend in der Zeitreihe?
- Wieviel Varianz wird durch diese Komponenten beschrieben?
- Welche Komponente beschreibt die meiste Varianz?
- Wie sieht die starre Saisonfigur aus?
- Hat sich die Saisonfigur signifikant geändert?
- Wie hat sich die Saisonfigur geändert (Amplitude, Phasenlage)?
- Welche Form und Stärke haben die signifikanten linearen bzw.
nichtlinearen Trends?




Nächste Seite: Glatte (tieffrequente) Komponente
Aufwärts: Suche nach speziellen Zusammenhängen
Vorherige Seite: Trendkomponente
Inhalt
ich
2000-01-24