Trendkomponente

Als Trendkomponente werden hier lineare und nicht-lineare Trends bis zur fünften Ordnung untersucht, d.h. es werden folgende fünf Ansätze verwendet:

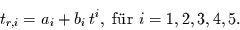$$t_{r,i} = a_{i} + b_{i}\,t^{i}, \mbox{ f\uml {u}r } i= 1,2,3,4,5.$$ (4.13)

Davon werden nur diejenigen Terme berücksichtigt, die signifikant in der Reihe enthalten sind, d.h. einen signifikanten Beitrag zu deren Varianz leisten. Wesentlich ist hierbei, daß jeder Term einzeln (univariate Korrelation bzw. Regression) eingeht. Dadurch bleibt die glatte (nicht Trend-) Komponente unberücksichtigt (es gibt keine Wendepunkte). Trägt keiner der Terme signifikant zur Varianz der Reihe bei, so besitzt sie keinen signifikanten Trend. Trägt nur der Term mit i=1 bei, so ist ein signifikanter linearer Trend gefunden, tragen auch (oder nur) Terme höherer Ordnung bei, so ist ein signifikanter nichtlinearer Trend gefunden, der progressiv oder degressiv steigend oder fallend sein kann. Da die Durchführung der Regression in Form einer Rekursion gemeinsam mit der saisonalen Komponente durchgeführt wird, wird sie im nächsten Abschnitt gemeinsam mit der Anpassung der saisonalen Komponente erläutert. Die Untersuchung von nichtlinearen Trends bis zur fünften Ordnung ist analog zur Untersuchung der glatten Komponente (ohne Trend) gewählt und wird in dem entsprechenden Abschnitt diskutiert.