



Nächste Seite: Gleichläufigkeit
Aufwärts: Spezielle statistische Methoden
Vorherige Seite: Spezielle statistische Methoden
Inhalt
Betrachtet man zunächst die gewöhnliche Standardabweichung, so stellt man
fest, daß sie nichts darüber aussagt, welche Strukturen die Varianz
der Zeitreihe hat. Aus der gewöhnlichen Statistik kennt man den
Variationskoeffizienten 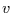 , der als das Verhältnis der Standardabweichung
, der als das Verhältnis der Standardabweichung
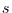 zum Mittelwert
zum Mittelwert 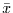 definiert ist. Er ist also ein Maß für die
Stärke der Schwankungen im Verhältnis zum Mittelwert. Dies ist allerdings
ein Maß für die gesamte Reihe und somit ein globales Maß. In der
Dendrochronologie wird sehr ähnlich dazu ein lokales Maß der
relativen Variabilität definiert, das jährliche Sensitivität
definiert ist. Er ist also ein Maß für die
Stärke der Schwankungen im Verhältnis zum Mittelwert. Dies ist allerdings
ein Maß für die gesamte Reihe und somit ein globales Maß. In der
Dendrochronologie wird sehr ähnlich dazu ein lokales Maß der
relativen Variabilität definiert, das jährliche Sensitivität 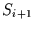 des Jahres
des Jahres 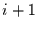 heißt. Somit kann jeder Zeitreihe eine Reihe der
jährlichen Sensitivität zugeordnet werden. Sie ist definiert, als die
Differenz zwischen dem Wert des
heißt. Somit kann jeder Zeitreihe eine Reihe der
jährlichen Sensitivität zugeordnet werden. Sie ist definiert, als die
Differenz zwischen dem Wert des 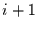 -ten Jahres zu dem des Vorjahres
geteilt durch den
Mittelwert der beiden Jahre. Daraus ergibt sich für die jährliche
Sensitivität:
-ten Jahres zu dem des Vorjahres
geteilt durch den
Mittelwert der beiden Jahre. Daraus ergibt sich für die jährliche
Sensitivität:
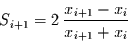 |
(6.1) |
Weiter kann man daraus zu einem globalen Maß der Zeitreihe gelangen, indem
man das arithmetische Mittel der Reihe 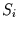 betrachtet. Dies führt
zur sogenannten mittleren Sensitivität:
betrachtet. Dies führt
zur sogenannten mittleren Sensitivität:
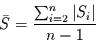 |
(6.2) |
wobei 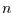 die Länge der Originalreihe (nicht der um
die Länge der Originalreihe (nicht der um 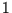 kürzeren Reihe der
jährlichen Sensitivität) ist.
Was unterscheidet nun die mittlere Sensitivität vom Variationskoeffizienten?
Zunächst sind beide ein Maß das Variation im Verhältnis zum Mittel
ausdrückt. Der Unterschied liegt nur darin, daß die mittlere Sensitivität
um so größer wird, je stärker die Gesamtvariabilitat durch die
Jahr-zu-Jahr-Variabilität bestimmt ist.
Ein Beispiel soll dies verdeutlichen.
Nehmen wir eine Zeitreihe
kürzeren Reihe der
jährlichen Sensitivität) ist.
Was unterscheidet nun die mittlere Sensitivität vom Variationskoeffizienten?
Zunächst sind beide ein Maß das Variation im Verhältnis zum Mittel
ausdrückt. Der Unterschied liegt nur darin, daß die mittlere Sensitivität
um so größer wird, je stärker die Gesamtvariabilitat durch die
Jahr-zu-Jahr-Variabilität bestimmt ist.
Ein Beispiel soll dies verdeutlichen.
Nehmen wir eine Zeitreihe 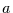 bestehend
aus
bestehend
aus 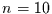 Werten, von denen die ersten fünf den Wert neun haben und die zweiten
fünf den Wert elf. Dann ist
Werten, von denen die ersten fünf den Wert neun haben und die zweiten
fünf den Wert elf. Dann ist 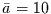 und die Standardabweichung
und die Standardabweichung
führt zu einem Wert von 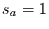 .
Nehmen wir nun eine andere Zeitreihe
.
Nehmen wir nun eine andere Zeitreihe 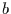 mit
mit 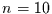 Werten, wobei die Zahlen
neun und elf immer alternierend auftreten sollen. Diese Reihe hat den
Mittelwert
Werten, wobei die Zahlen
neun und elf immer alternierend auftreten sollen. Diese Reihe hat den
Mittelwert 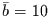 und die Standardabweichung
und die Standardabweichung 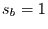 .
Wie wir also sehen, haben beide Reihen den gleichen Mittelwert und die
gleiche Standardabweichung, und demnach auch einen gleichen Variationskoeffizient.
Wie sieht es nun mit den Sensitivitäten der Reihen aus?
Aus Gleichung B.1 folgt für die Reihen der jährlichen Sensitivität:
.
Wie wir also sehen, haben beide Reihen den gleichen Mittelwert und die
gleiche Standardabweichung, und demnach auch einen gleichen Variationskoeffizient.
Wie sieht es nun mit den Sensitivitäten der Reihen aus?
Aus Gleichung B.1 folgt für die Reihen der jährlichen Sensitivität:
Das ergibt folgende mittleren Sensitivitäten:
Das Beispiel zeigt deutlich, daß die Sensitivität ein Maß für die
Jahr-zu-Jahr-Variabilität ist, die ja in der zweiten Reihe
(alternierende Werte) besonders hoch, in der ersten hingegen besonders
niedrig ist.
Wie der Variationskoeffizient ist aber auch die Sensitivität nicht
invariant gegenüber Mittelwerttransformationen. Während also die
Standaradabweichung (und im allgemeinen auch alle anderen grundlegenden
statistischen Variationsmaße) nicht vom Mittlewert abhängen, gilt dies
für den Variationskoeffizient und die Sensitivität nicht. Hat eine
Zeitreihe den Mittelwert null, so ist kein Variationskoeffizient definierbar.
Für die jährliche Sensitivität gilt diese Eigenschaft schon lokal, d.h.
es darf in der Zeitreihe nirgends
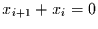 auftreten. Hätte man
obiges Beispiel mit Reihen der Werte
auftreten. Hätte man
obiges Beispiel mit Reihen der Werte 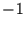 und
und 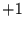 anstatt
anstatt 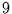 und
und 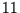 versucht, so wäre man schnell auf nicht hebbare Singularitäten gestoßen.
Daraus folgt, daß man Sensitivitäten keinesfalls für normierte Reihen
(d.h. Mittelwert
versucht, so wäre man schnell auf nicht hebbare Singularitäten gestoßen.
Daraus folgt, daß man Sensitivitäten keinesfalls für normierte Reihen
(d.h. Mittelwert 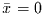 und Standardabweichung
und Standardabweichung 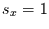 )
berechnen darf.
Die Berechnung der Sensitivität ist günstig zum
Vergleich von Baumringdaten, da diese positiv definit sind. Man kann beim
Vergleich verschiedener Datenreihen mit etwa gleichem Mittelwert, oder
beim Vergleich von auf gleichen Mittelwert gebrachten Datenreihen die
Sensitivität nutzen, da sie dann aussagt, welche Reihe größere
Jahr-zu-Jahr-Schwankungen aufweist.
)
berechnen darf.
Die Berechnung der Sensitivität ist günstig zum
Vergleich von Baumringdaten, da diese positiv definit sind. Man kann beim
Vergleich verschiedener Datenreihen mit etwa gleichem Mittelwert, oder
beim Vergleich von auf gleichen Mittelwert gebrachten Datenreihen die
Sensitivität nutzen, da sie dann aussagt, welche Reihe größere
Jahr-zu-Jahr-Schwankungen aufweist.




Nächste Seite: Gleichläufigkeit
Aufwärts: Spezielle statistische Methoden
Vorherige Seite: Spezielle statistische Methoden
Inhalt
ich
2000-01-24