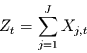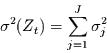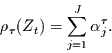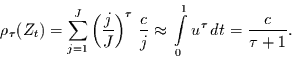Nächste Seite: Numerische Untersuchungen
Aufwärts: Prozesse mit langem Gedächtnis
Vorherige Seite: Zusammenhänge zwischen den Maßen
Inhalt
Eine Näherung einer Realisation eines FIWN-Prozesses kann mit Hilfe der
AR( - oder MA(
- oder MA(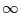 )-Darstellung des fraktionellen Integrierens
von weißem Rauschen erzeugt werden. Dies ist sehr aufwendig, so daß ich
eine Erzeugung mit Hilfe von Surrogat-Daten bevorzugen würde.
Dies ist z.B. mit der Weierstraßschen Sinusfunktion
)-Darstellung des fraktionellen Integrierens
von weißem Rauschen erzeugt werden. Dies ist sehr aufwendig, so daß ich
eine Erzeugung mit Hilfe von Surrogat-Daten bevorzugen würde.
Dies ist z.B. mit der Weierstraßschen Sinusfunktion
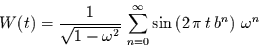 |
(52) |
möglich. Diese Funktion erzeugt bei 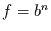 eine Spektrallinie mit
eine Spektrallinie mit
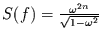 . Mit
. Mit 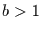 ,
, 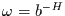 und
und 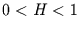 folgt für das Spektrum an den Spektrallinien
folgt für das Spektrum an den Spektrallinien
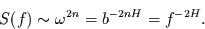 |
(53) |
Man beachte, daß das kumulative kontinuierliche Spektrum eines fraktionell
integrierten Prozesses mit
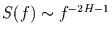 die Form
die Form
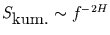 hat.
Eine andere Möglichkeit zumindest einen Prozeß
hat.
Eine andere Möglichkeit zumindest einen Prozeß 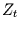 mit
mit 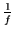 -Rauschen zu erzeugen (s. [1]),
liegt darin, die Summe über
-Rauschen zu erzeugen (s. [1]),
liegt darin, die Summe über 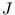 unabhängige AR(1)-Prozesse
unabhängige AR(1)-Prozesse 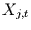 zu bilden, d.h. es gelte
zu bilden, d.h. es gelte
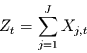 |
(54) |
und
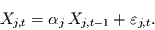 |
(55) |
Die
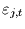 sollen dabei unabhängige WN-Prozesse sein, die der
Einfachheit halber um null zentriert sind und jeweils die Varianz
sollen dabei unabhängige WN-Prozesse sein, die der
Einfachheit halber um null zentriert sind und jeweils die Varianz
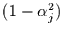 haben. Dann gilt
haben. Dann gilt
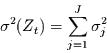 |
(56) |
und
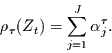 |
(57) |
Um die Gesamtvarianz in Grenzen zu halten, kann man einfach
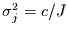 annehmen. Unterstellt man weiter, daß die Koeffizienten
annehmen. Unterstellt man weiter, daß die Koeffizienten 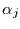 im
Intervall (0,1) ungefähr gleich-verteilt sind, so gilt für die
Autokorrelationsfunktion approximativ
im
Intervall (0,1) ungefähr gleich-verteilt sind, so gilt für die
Autokorrelationsfunktion approximativ
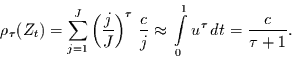 |
(58) |
Da 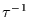 nicht absolut summierbar ist, ist es
auch
nicht absolut summierbar ist, ist es
auch
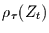 nicht. Damit ist gezeigt, daß
nicht. Damit ist gezeigt, daß 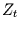 ein
Prozeß mit langem Gedächtnis ist.
Dieser ist erzeugt worden, aus der endlichen Summe von Prozessen, deren
Autokorrelationsfunktion mit
ein
Prozeß mit langem Gedächtnis ist.
Dieser ist erzeugt worden, aus der endlichen Summe von Prozessen, deren
Autokorrelationsfunktion mit
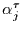 ging, also aus Prozessen
mit kurzem Gedächtnis.
ging, also aus Prozessen
mit kurzem Gedächtnis.




Nächste Seite: Numerische Untersuchungen
Aufwärts: Prozesse mit langem Gedächtnis
Vorherige Seite: Zusammenhänge zwischen den Maßen
Inhalt
ich
2000-01-25