



Nächste Seite: Analyse von Beobachtungszeitreihen
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Cantor-Dust-Methode
Inhalt
In Tabelle 2 werden
alle Ergebnisse nebeneinandergestellt.
Tabelle:
Zusammenfassung der Ergebnisse der Untersuchung künstlicher Reihen.
WN bedeutet White Noise
| Zeitreihe |
Gau |
AR1 |
Bro |
|---|
| Wahrer Wert |
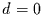 |
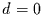 |
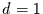 |
| Stationarität |
stat. |
stat. |
nicht stat. |
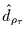 |
0 |
keine Aussage |
keine Aussage |
| WN-Test |
WN |
kein WN |
kein WN |
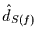 |
0 |
keine Aussage |
.92 |
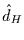 |
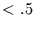 |
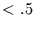 |
1.06 |
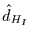 |
.04 |
.1 |
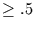 |
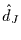 |
.1 |
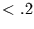 |
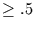 |
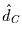 |
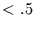 |
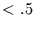 |
1.15 |
Man sieht, daß keines der angewendeten Methoden die in allen Fällen beste
Methode ist. Desweiteren kann man schließen, daß die klassischen
Untersuchungen unbedingt durchgeführt werden sollten, um die Ergebnisse der
moderneren Methoden besser interpretieren zu können. So erkennt man
z.B. sowohl an der Autokorrelationsfunktion als auch am Spektrum das
weiße Rauschen, d.h. 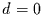 , was von
, was von 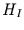 und
und 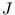 mit .04
und .1 leicht überschätzt wird. Die Frage, ob
mit .04
und .1 leicht überschätzt wird. Die Frage, ob 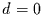 ist
oder nicht, ist aber die Frage,
ob die Zeitreihe aus einem Prozeß mit langem Gedächtnis stammt oder nicht.
Werte von
ist
oder nicht, ist aber die Frage,
ob die Zeitreihe aus einem Prozeß mit langem Gedächtnis stammt oder nicht.
Werte von 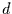 , die nahe bei 0 liegen, sollte man deshalb nur mit Vorsicht
interpretieren.
, die nahe bei 0 liegen, sollte man deshalb nur mit Vorsicht
interpretieren.




Nächste Seite: Analyse von Beobachtungszeitreihen
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Cantor-Dust-Methode
Inhalt
ich
2000-01-25