



Nächste Seite: Zusammenfassung der Ergebnisse
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Hurst-Exponent
Inhalt
Mit der Cantor-Dust-Methode
wird die Dimension der Niveaumenge des Mittelwertes
jeder Zeitreihe geschätzt. Dabei werden Subintervalle von der Länge eines
Zeitschrittes bis zur Länge von 100 Zeitschritten zugelassen.
Der Verlauf von 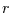 in Abhängigkeit von der Länge des Zeitfensters ist in
Abbildung 8 gegeben. Zusätzlich ist dort der Schätzwert des
Exponenten
in Abhängigkeit von der Länge des Zeitfensters ist in
Abbildung 8 gegeben. Zusätzlich ist dort der Schätzwert des
Exponenten 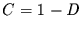 in Abhängigkeit der berücksichtigten Fensterbreiten dargestellt.
Es ist klar zu erkennen, daß sowohl für die Reihe Gau, als auch
für die Reihe AR1 der Exponent gegen null konvergiert. Damit werden
diese Reihen als nicht skaleninvariant erkannt. Für sie wird also
in Abhängigkeit der berücksichtigten Fensterbreiten dargestellt.
Es ist klar zu erkennen, daß sowohl für die Reihe Gau, als auch
für die Reihe AR1 der Exponent gegen null konvergiert. Damit werden
diese Reihen als nicht skaleninvariant erkannt. Für sie wird also
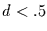 richtig erkannt. Es gibt keine Clusterung der
Schnitte der Niveaulinie. Für die Reihe Bro
konvergiert der Exponent gegen .65, was einer Dimension der Niveaumenge von
.35 entspricht. Hier also sehen wir eine Clusterung der Ereignisse. Zwar
hat die Methode das lange Gedächtnis der instationären Reihe erkannt, den
Zahlenwert mit .65 aber um 15% überschätzt.
richtig erkannt. Es gibt keine Clusterung der
Schnitte der Niveaulinie. Für die Reihe Bro
konvergiert der Exponent gegen .65, was einer Dimension der Niveaumenge von
.35 entspricht. Hier also sehen wir eine Clusterung der Ereignisse. Zwar
hat die Methode das lange Gedächtnis der instationären Reihe erkannt, den
Zahlenwert mit .65 aber um 15% überschätzt.
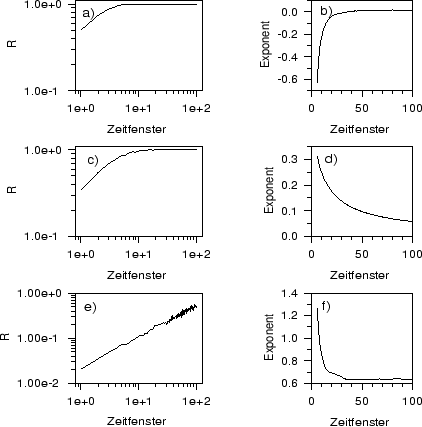
Abbildung:
Anzahl der Schnitte eines Niveaus in Abhängigkeit vom Zeitfenster
bei Zeitreihen mit jeweils 2000 Werten aus
(a) weißen, (c) roten und (e)
Brownschen Rauschen in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für das (b) weiße, (d) rote und (f) Brownsche Rauschen.
 |




Nächste Seite: Zusammenfassung der Ergebnisse
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Hurst-Exponent
Inhalt
ich
2000-01-25

