



Nächste Seite: Cantor-Dust-Methode
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Strukturfunktion
Inhalt
Für alle drei Reihen und alle Zeitverschiebungen bis
200 wird der Hurst-Exponent berechnet. Zweihundert Zeitverschiebungen
entsprechen wieder 10 unabhängigen Intervallen.
In Abbildung 7 ist sowohl 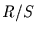 gegen die Zeitspanne
gegen die Zeitspanne 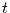 doppelt-logarithmisch dargestellt, als auch die Steigung der besten linearen
Anpassung.
Zwar sieht die Abhängigkeit
von
doppelt-logarithmisch dargestellt, als auch die Steigung der besten linearen
Anpassung.
Zwar sieht die Abhängigkeit
von 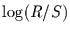 von der Zeitspanne
von der Zeitspanne 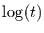 in allen drei Fällen linear
aus, jedoch nimmt sowohl im Fall der Reihe Gau, als auch im Fall der
Reihe AR1 die Steigung kontinuierlich von Werten über .7 ab auf
etwa .6 im Fall der Reihe Gau und etwa .7 im Fall der Reihe
AR1. Theoretisch sollte für beide Reihen der Wert .5 beobachtet
werden. Für die Reihe Bro konvergiert der Hurst-Exponent von unten
gegen
in allen drei Fällen linear
aus, jedoch nimmt sowohl im Fall der Reihe Gau, als auch im Fall der
Reihe AR1 die Steigung kontinuierlich von Werten über .7 ab auf
etwa .6 im Fall der Reihe Gau und etwa .7 im Fall der Reihe
AR1. Theoretisch sollte für beide Reihen der Wert .5 beobachtet
werden. Für die Reihe Bro konvergiert der Hurst-Exponent von unten
gegen 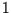 . Und da dies der theoretisch zu erwartende Wert ist, kann man damit
zufrieden sein.
. Und da dies der theoretisch zu erwartende Wert ist, kann man damit
zufrieden sein.
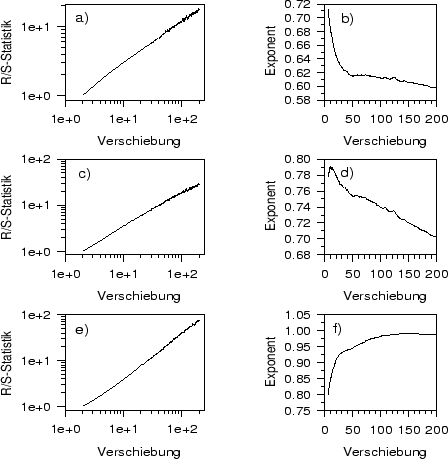
Abbildung:
Hurst-Exponenten von Zeitreihen mit jeweils 2000 Werten aus
(a) weißen, (c) roten und (e)
Brownschen Rauschen in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für das (b) weiße, (d) rote und (f) Brownsche Rauschen.
 |




Nächste Seite: Cantor-Dust-Methode
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Strukturfunktion
Inhalt
ich
2000-01-25

