



Nächste Seite: Hurst-Exponent
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Spektrum
Inhalt
Die Strukturfunktion 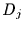 zur Verschiebung
zur Verschiebung 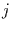 wird für alle Zeitreihen nach Gleichung (30) berechnet. Diese
Anwendung auf nichtintegrierte Zeitreihen erlaubt es
wird für alle Zeitreihen nach Gleichung (30) berechnet. Diese
Anwendung auf nichtintegrierte Zeitreihen erlaubt es 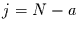 Verschiebungen
zu betrachten, wenn
Verschiebungen
zu betrachten, wenn 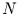 die Zeitreihenlänge ist, und
die Zeitreihenlänge ist, und 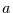 die Anzahl der
Schätzwerte, die in die quadratische Mittelung eingehen sollen. Wir können
damit, wenn wir mindestens 100 Realisierungen voraussetzen,
bis zu einer Zeitverschiebung von 1900 vorgehen.
Nun kann man
die Anzahl der
Schätzwerte, die in die quadratische Mittelung eingehen sollen. Wir können
damit, wenn wir mindestens 100 Realisierungen voraussetzen,
bis zu einer Zeitverschiebung von 1900 vorgehen.
Nun kann man 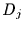 gegen
gegen
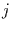 in der Log-Log-Darstellung auftragen und eine lineare Regression
durchführen. Die Ergebnisse sind in Abbildung 5 dargestellt.
Dabei enthalten die Teile a),c) und e) die Strukturfunktion der
Zeitreihen, während b),d) und f) die Steigung der
besten angepaßten Geraden bis zu der jeweils angegebenen Verschiebung
zeigt. Da sich für größere Zeitverschiebungen keine nennenswerten
Änderungen ergeben, werden die Ergebnisse nur für die ersten 200
Zeitverschiebungen dargestellt. Sowohl für die Reihe Gau, als auch
für die Reihe AR1 geht die Strukturfunktion sehr schnell gegen
die Wurzel aus 2, was nach Gleichung (31) zu erwarten ist.
Beide Reihen werden also eindeutig als Realisationen von Prozessen ohne
langes Gedächtnis mit
in der Log-Log-Darstellung auftragen und eine lineare Regression
durchführen. Die Ergebnisse sind in Abbildung 5 dargestellt.
Dabei enthalten die Teile a),c) und e) die Strukturfunktion der
Zeitreihen, während b),d) und f) die Steigung der
besten angepaßten Geraden bis zu der jeweils angegebenen Verschiebung
zeigt. Da sich für größere Zeitverschiebungen keine nennenswerten
Änderungen ergeben, werden die Ergebnisse nur für die ersten 200
Zeitverschiebungen dargestellt. Sowohl für die Reihe Gau, als auch
für die Reihe AR1 geht die Strukturfunktion sehr schnell gegen
die Wurzel aus 2, was nach Gleichung (31) zu erwarten ist.
Beide Reihen werden also eindeutig als Realisationen von Prozessen ohne
langes Gedächtnis mit 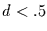 erkannt.
Für die Reihe Bro sieht man einen
signifikanten linearen Anstieg. Das bedeutet, daß der dahinterstehende
Prozeß als ein Prozeß mit langem Gedächtnis und
erkannt.
Für die Reihe Bro sieht man einen
signifikanten linearen Anstieg. Das bedeutet, daß der dahinterstehende
Prozeß als ein Prozeß mit langem Gedächtnis und
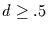 erkannt wird. Der Exponent
erkannt wird. Der Exponent
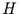 wird auf Werte zwischen .5 und .57 geschätzt, also unweit des wahren
Wertes .5.
wird auf Werte zwischen .5 und .57 geschätzt, also unweit des wahren
Wertes .5.
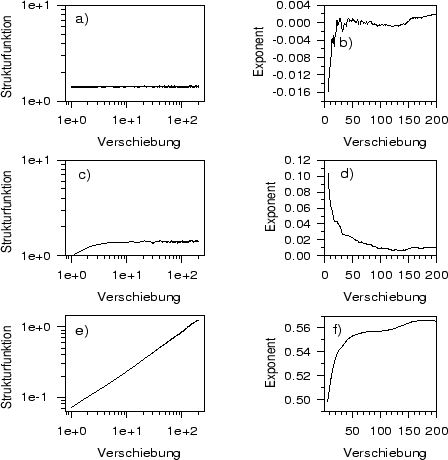
Abbildung:
Strukturfunktionen von Zeitreihen mit jeweils 2000 Werten aus
(a) weißen, (c) roten und (e)
Brownschen Rauschen in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für das (b) weiße, (d) rote und (f) Brownsche Rauschen.
 |
Alternativ
wird die Strukturfunktion der integrierten Reihen für
nichtüberlappende Teilintervalle berechnet. Letzteres hat
zur Folge, daß die Anzahl der Freiheitsgrade nicht so stark überschätzt
wird, wie es bei Verwendung von Gleichung (39) der Fall wäre.
Bei Zeitreihen der Länge 2000
besteht dann die Strukturfunktion der integrierten Reihen
zur Verschiebung 100 nur noch aus dem Mittel von
zwanzig Werten, die dafür aber voneinander unabhängig sind.
Nun kann man auch 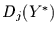 gegen
gegen
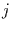 in der Log-Log-Darstellung auftragen und eine lineare Regression
durchführen um den Exponenten
in der Log-Log-Darstellung auftragen und eine lineare Regression
durchführen um den Exponenten 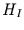 zu erhalten.
Die Ergebnisse sind in Abbildung 6 dargestellt.
Dabei enthalten die Teile a),c) und e) die Strukturfunktion der
(integrierten) Zeitreihen, während b),d) und f) die Steigung der
besten angepaßten Geraden bis zu der jeweils angegebenen Verschiebung
zeigt.
Wir sehen, daß der lineare Zusammenhang
zu erhalten.
Die Ergebnisse sind in Abbildung 6 dargestellt.
Dabei enthalten die Teile a),c) und e) die Strukturfunktion der
(integrierten) Zeitreihen, während b),d) und f) die Steigung der
besten angepaßten Geraden bis zu der jeweils angegebenen Verschiebung
zeigt.
Wir sehen, daß der lineare Zusammenhang
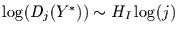 in allen drei Fällen sehr gut gegeben ist.
Der Koeffizient
in allen drei Fällen sehr gut gegeben ist.
Der Koeffizient 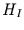 wird
jedoch sowohl für das weiße Rauschen, als auch für das rote Rauschen
mit .55 und .58 etwas zu hoch
geschätzt8.
Andererseits wird das Brownsche Rauschen
mit dem theoretischen Wert 1 knapp unterschätzt.
wird
jedoch sowohl für das weiße Rauschen, als auch für das rote Rauschen
mit .55 und .58 etwas zu hoch
geschätzt8.
Andererseits wird das Brownsche Rauschen
mit dem theoretischen Wert 1 knapp unterschätzt.
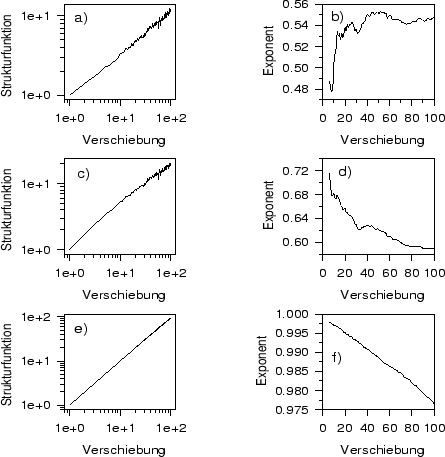
Abbildung:
Strukturfunktionen von integrierten Zeitreihen mit jeweils 2000 Werten aus
(a) weißen, (c) roten und (e)
Brownschen Rauschen in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für das (b) weiße, (d) rote und (f) Brownsche Rauschen.
 |




Nächste Seite: Hurst-Exponent
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Spektrum
Inhalt
ich
2000-01-25


