Spektrum

Für alle drei Zeitreihen wurde die spektrale Dichte geschätzt. Ein Kolmogoroff-Smirnoff-Test und ein Anderson-Darling-Test (s. [14]) lehnen die Hypothese des weißen Rauschens sowohl für die Reihe AR1 als auch für die Reihe Bro mit über 99% Signifikanz ab. Die Reihe Gau ist nicht vom weißen Rauschen unterscheidbar. Ein Fisher-Test [14] auf signifikante harmonische Anteile findet keine signifikante Schwingung bei der Zeitreihe Gau, eine höchst signifikante Schwingung bei der Zeitreihe AR1 bei der Periode von 400 Jahren und eine höchst signifikante Schwingung bei der Zeitreihe Bro bei 2000 Jahren. Dieser Test basiert auf der Annahme eines weißen Rauschens und ist demnach bei den Zeitreihen, bei denen er signifikante Schwingungen erkennt, nicht anwendbar. Jedoch deuten signifikante tiefe Frequenzen schon darauf hin, daß tiefe Frequenzen bevorzugt vorkommen. Im nächsten Schritt kann man die spektrale Dichte der Zeitreihen für Frequenzen kleiner als .1 aufzeichnen und mittels linearer Regression eine Gerade optimal anpassen. Dies ist für die drei Zeitreihen in Abbildung 4 geschehen. Zusätzlich ist noch ein AR(1)-Prozeß optimal an das jeweilige Spektrum angepaßt. Im Fall der Reihe Gau ist der optimal angepaßte AR(1)-Prozeß das weiße Rauschen. Auch die optimal angepaßte Gerade zeigt keine signifikante Steigung. Dies bestätigt, daß es sich bei der Reihe Gau um weißes Rauschen handelt. Das Spektrum der Reihe AR1 zeigt keine so eindeutige Zuordnung. Zwar erklärt die Gerade nur 4.7% der Varianz des Spektrums, jedoch sind ungeglättete Spektralschätzer immer sehr variationsfreudig. Zwischen dem Spektrum eines optimal angepaßten autoregressiven Prozesses erster Ordnung und einem FIWN-Prozeß scheint man nicht so leicht unterscheiden zu können (vergl. Abb. 4). Ganz anders ist das beim Spektrum der Reihe Bro, die recht gut (75% erklärte Varianz) durch eine Gerade in der Log-Log-Darstellung repräsentiert ist. Die Steigung der optimal angepaßten Gerade beträgt -1.84, was gleichbedeutend ist mit einem besten Schätzer für den Exponenten 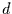$d$ eines FIWN-Prozesses von .92. Dieser Schätzer ist nur knapp (10%) unter dem wahren Wert von 1 für das Brownsche Rauschen. Abbildung 4c zeigt jedoch klar, daß der optimal angepaßte AR(1)-Prozeß keine sinnvolle Beschreibung der Zeitreihe darstellt.

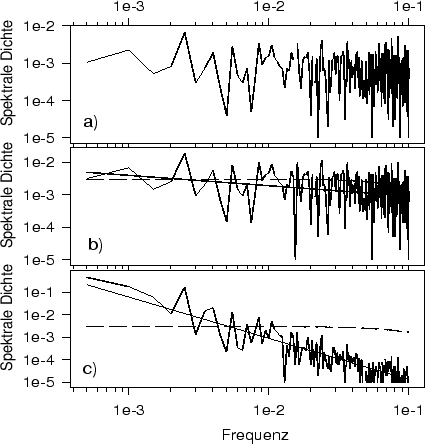
Abbildung: Spektren von Zeitreihen mit jeweils 2000 Werten aus (a) weißen, (b) roten und (c) Brownschen Rauschen in Log-Log-Darstellung. Die Geraden sind optimal angepaßt. Die unterbrochenen Linien entsprechen optimal angepaßten AR(1)-Prozessen.