



Nächste Seite: Spektrum
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Die Zeitreihen
Inhalt
Für alle drei Reihen wird die Autokorrelationsfunktion berechnet.
Für Gau ist die Autokorrelationsfunktion bei keiner
Verschiebung signifikant von null zu unterscheiden. Gau wird
demnach eindeutig als weißes Rauschen erkannt. Bei AR1 ist die
Autokorrelationsfunktion für die ersten 9 Verschiebungen signifikant
(95%) von null zu unterscheiden, d.h. nur diese 9 Werte stehen zur
Analyse zur
Verfügung. Führt man eine lineare Regression gemäß
Gleichung (28) durch, so erhält man als besten Schätzer für
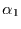 den Wert
den Wert
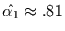 . Die Korrelation erklärt aber
nur 70% der Varianz der 9 Schätzer der Autokorrelationsfunktion. Gemäß
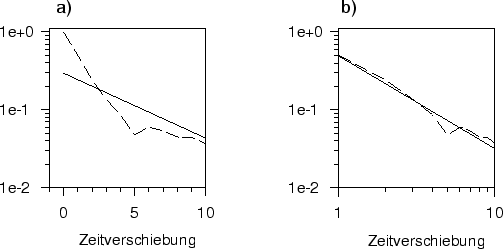
Abbildung 2a scheint die lineare Beziehung zwischen dem
Logarithmus der Autokorrelation und der Zeitverschiebung für die ersten 5
Werte am besten gegeben zu sein. Dort liefert eine lineare Regression
einen besten Schätzer von
. Die Korrelation erklärt aber
nur 70% der Varianz der 9 Schätzer der Autokorrelationsfunktion. Gemäß
Abbildung 2a scheint die lineare Beziehung zwischen dem
Logarithmus der Autokorrelation und der Zeitverschiebung für die ersten 5
Werte am besten gegeben zu sein. Dort liefert eine lineare Regression
einen besten Schätzer von
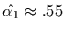 mit einer
erklärten Varianz von 99%. Der lineare Zusammenhang wird zwar
schön gesehen,
aber der Schätzer liegt immer noch um 10% neben dem wahren Wert. Letzterer
wird am besten getroffen, wenn man
mit einer
erklärten Varianz von 99%. Der lineare Zusammenhang wird zwar
schön gesehen,
aber der Schätzer liegt immer noch um 10% neben dem wahren Wert. Letzterer
wird am besten getroffen, wenn man
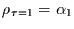 als Schätzer
verwendet. Man erhält dann
als Schätzer
verwendet. Man erhält dann
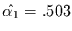 mit einem
90%-Konfidenzintervall von
mit einem
90%-Konfidenzintervall von ![$[.47;.53]$](img224.gif) . Wen dieses Ergebnis betrübt, der
wird noch enttäuschter sein, wenn er sich Abbildung 2b ansieht,
in der die Autokorrelationsfunktion für die ersten zehn Verschiebungen
in der Log-Log-Darstellung gegeben ist. Die Log-Log-Darstellung der
signifikanten Werte ist
besser durch eine Gerade repräsentiert als die Log-Lin-Darstellung, d.h.
es wird nicht nur der Wert von
. Wen dieses Ergebnis betrübt, der
wird noch enttäuschter sein, wenn er sich Abbildung 2b ansieht,
in der die Autokorrelationsfunktion für die ersten zehn Verschiebungen
in der Log-Log-Darstellung gegeben ist. Die Log-Log-Darstellung der
signifikanten Werte ist
besser durch eine Gerade repräsentiert als die Log-Lin-Darstellung, d.h.
es wird nicht nur der Wert von 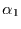 schlecht geschätzt,
sondern
es wird auch der durchaus einfache AR(1)-Prozeß nicht als solcher
erkannt. Die Gerade
in der Log-Log-Darstellung erklärt 74 Prozent der Varianz, während in der
Log-Lin-Darstellung nur 70 Prozent der Varianz durch die Gerade erklärt werden.
Dies spricht dafür, daß die Zeitreihe eine Realisation eines Prozesses mit
langem Gedächtnis ist. Der Schätzwert für den Exponenten
schlecht geschätzt,
sondern
es wird auch der durchaus einfache AR(1)-Prozeß nicht als solcher
erkannt. Die Gerade
in der Log-Log-Darstellung erklärt 74 Prozent der Varianz, während in der
Log-Lin-Darstellung nur 70 Prozent der Varianz durch die Gerade erklärt werden.
Dies spricht dafür, daß die Zeitreihe eine Realisation eines Prozesses mit
langem Gedächtnis ist. Der Schätzwert für den Exponenten 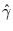 beträgt dann 1.19. Daraus würde
beträgt dann 1.19. Daraus würde
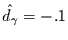 folgen.
folgen.
Abbildung 2:
Autokorrelationsfunktion einer
Zeitreihe aus 2000 Daten eines AR(1)-Prozesses mit 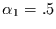 (a) in der Log-Lin-Darstellung und (b) in der Log-Log-Darstellung.
(a) in der Log-Lin-Darstellung und (b) in der Log-Log-Darstellung.
 |
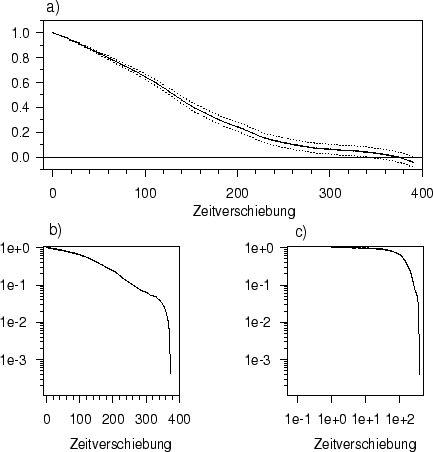
In Abbildung 3 ist die Autokorrelation der Reihe Bro
in der Lin-Lin-, der Log-Lin- und der Log-Log-Darstellung angegeben.
Da diese Reihe als instationär erkannt wurde,
darf Abbildung 3 nicht interpretiert werden.
Abbildung 3:
Autokorrelationsfunktion einer
Zeitreihe aus 2000 Daten eines Brownschen Rauschens
(a) in der Lin-Lin-Darstellung (mit 90% Konfidenzintervall),
(b) in der Log-Lin-Darstellung
und (c) in der Log-Log-Darstellung.
 |




Nächste Seite: Spektrum
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Die Zeitreihen
Inhalt
ich
2000-01-25


