



Nächste Seite: Autokorrelationsfunktion
Aufwärts: Analyse künstlicher Zeitreihen
Vorherige Seite: Analyse künstlicher Zeitreihen
Inhalt
Die verschiedenen Maße werden nun an drei künstlichen Zeitreihen getestet.
Mit Hilfe der Numerical Recipes [13] wird eine Folge von
zweitausend Gauß-verteilten Zufallszahlen erzeugt7. Diese stellt eine
Zeitreihe von Gaußschem weißen Rauschen (Gau) dar. Mit Hilfe des Filters
aus Gleichung (2) entsteht dadurch eine Zeitreihe von Brownschem
Rauschen (Bro). Der Filter aus Gleichung (3) mit dem Parameter
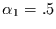 wird verwendet, um aus dem Gaußschen weißen Rauschen ein
Gaußsches rotes Rauschen (AR1) zu erzeugen. Da einige
Analyseverfahren auf der Existenz und Stationarität von Momenten bis
zur zweiten Ordnung basieren, werden alle Zeitreihen auf Instationaritäten in
der Varianz, dem Mittelwert und der Autokorrelationsfunktion hin untersucht.
Dazu werden die Zeitreihen jeweils in zwei Hälften geteilt und getestet, ob
sich die geschätzten Momente für die jeweiligen Hälften voneinander
unterscheiden.
Während bei der Zeitreihe Bro alle untersuchten Momente mit mehr
als 99.99% Wahrscheinlichkeit instationär sind, unterscheiden sich die
Varianzen zwischen der ersten und zweiten Hälfte bei den anderen Reihen
auf dem Niveau von 90%. Die Mittelwerte unterscheiden sich nicht.
wird verwendet, um aus dem Gaußschen weißen Rauschen ein
Gaußsches rotes Rauschen (AR1) zu erzeugen. Da einige
Analyseverfahren auf der Existenz und Stationarität von Momenten bis
zur zweiten Ordnung basieren, werden alle Zeitreihen auf Instationaritäten in
der Varianz, dem Mittelwert und der Autokorrelationsfunktion hin untersucht.
Dazu werden die Zeitreihen jeweils in zwei Hälften geteilt und getestet, ob
sich die geschätzten Momente für die jeweiligen Hälften voneinander
unterscheiden.
Während bei der Zeitreihe Bro alle untersuchten Momente mit mehr
als 99.99% Wahrscheinlichkeit instationär sind, unterscheiden sich die
Varianzen zwischen der ersten und zweiten Hälfte bei den anderen Reihen
auf dem Niveau von 90%. Die Mittelwerte unterscheiden sich nicht.
ich
2000-01-25