

Nächste Seite: Der Hurst-Exponent
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Das Spektrum
Inhalt
Die Strukturfunktion
Weder das Spektrum, noch die Autokorrelationsfunktion sind gute Schätzer.
Einerseits wird die Autokorrelationsfunktion i.a.
relativ schnell unsignifikant
klein, andererseits ist das Spektrum kein erwartungstreuer, konsistenter
Schätzer. Darüberhinaus muß für die Schätzung dieser Größen
Stationarität des zugrundeliegenden Prozesses (d.h. 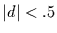 )
vorausgesetzt werden.
Nun kann man nach der quadratisch
gemittelten Differenz zweier Werte aus einer Zeitreihe
)
vorausgesetzt werden.
Nun kann man nach der quadratisch
gemittelten Differenz zweier Werte aus einer Zeitreihe 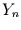 fragen, für den Fall, daß sie
fragen, für den Fall, daß sie 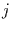 Zeitschritte auseinanderliegen.
Diese Funktion
Zeitschritte auseinanderliegen.
Diese Funktion
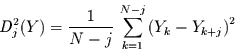 |
(30) |
heißt quadratische Strukturfunktion der Funktion 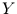 .
Strukturfunktionen werden schon lange in der Turbulenztheorie eingesetzt
(s. [17]), wo gezeigt
werden konnte, daß die Strukturfunktion sowohl für die Temperatur,
als auch für Feuchte und Windgeschwindigkeit im Inertialbereich
dem räumlichen Skalengesetz
.
Strukturfunktionen werden schon lange in der Turbulenztheorie eingesetzt
(s. [17]), wo gezeigt
werden konnte, daß die Strukturfunktion sowohl für die Temperatur,
als auch für Feuchte und Windgeschwindigkeit im Inertialbereich
dem räumlichen Skalengesetz
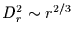 gehorcht.
Die (quadratische) Strukturfunktion hat in der
Literatur viele Namen, von denen
Fluktuationen,
mittlere quadratische Verschiebung und
mittlere quadratische Abweichung
nur eine kleine Auswahl darstellen.
Für einen autokovarianzstationären
Prozeß mit kurzem oder keinem Gedächtnis konvergiert die Strukturfunktion
bei zunehmendem
gehorcht.
Die (quadratische) Strukturfunktion hat in der
Literatur viele Namen, von denen
Fluktuationen,
mittlere quadratische Verschiebung und
mittlere quadratische Abweichung
nur eine kleine Auswahl darstellen.
Für einen autokovarianzstationären
Prozeß mit kurzem oder keinem Gedächtnis konvergiert die Strukturfunktion
bei zunehmendem 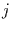 gegen
gegen
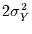 ,
was man aus Gleichung (30) leicht sieht:
,
was man aus Gleichung (30) leicht sieht:
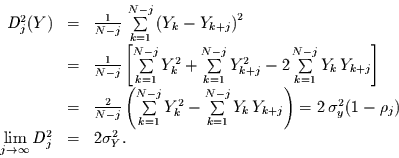 |
(31) |
Dann enthält die Strukturfunktion keine neue Information. Für Zeitreihen
aus Prozessen ohne Gedächtnis ist
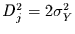 unabhängig von
unabhängig von 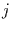 . Für Zeitreihen aus stationären
Prozessen mit kurzem Gedächtnis
und für Zeitreihen aus
stationären Prozessen mit langem Gedächtnis (
. Für Zeitreihen aus stationären
Prozessen mit kurzem Gedächtnis
und für Zeitreihen aus
stationären Prozessen mit langem Gedächtnis (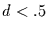 )
konvergiert
)
konvergiert 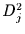 gegen
gegen
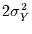 .
Die beiden letztgenannten
Prozesse können also von der Strukturfunktion nicht
unterschieden werden.
Für Prozesse mit langem Gedächtnis geht hingegen
.
Die beiden letztgenannten
Prozesse können also von der Strukturfunktion nicht
unterschieden werden.
Für Prozesse mit langem Gedächtnis geht hingegen
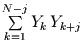 nicht unbedingt schnell gegen null.
Darüberhinaus kann für instationäre Prozesse
nicht unbedingt schnell gegen null.
Darüberhinaus kann für instationäre Prozesse
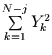 nicht gleich
nicht gleich
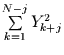 gesetzt werden.
Aus der Tatsache, daß die Strukturfunktion dann
immer weiter divergiert, kann man
den instationären Prozeß mit langem Gedächtnis (d.h.
gesetzt werden.
Aus der Tatsache, daß die Strukturfunktion dann
immer weiter divergiert, kann man
den instationären Prozeß mit langem Gedächtnis (d.h. 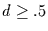 )
erkennen. Dies ist eine für die
Zeitreihenanalyse wichtige Erkenntnis.
Für die Brownsche Diffusion ist der Erwartungswert für
)
erkennen. Dies ist eine für die
Zeitreihenanalyse wichtige Erkenntnis.
Für die Brownsche Diffusion ist der Erwartungswert für 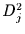 durch die Einstein-Relation [9]
durch die Einstein-Relation [9]
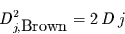 |
(32) |
gegeben.3
Dabei ist 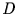 eine Diffussionskonstante.
Wir können demnach für ein Brownsches Rauschen schreiben
eine Diffussionskonstante.
Wir können demnach für ein Brownsches Rauschen schreiben
 |
(33) |
Für andere Prozesse mit langem Gedächtnis kann man nun
die Einstein-Relation verallgemeinern, indem man
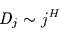 |
(34) |
ansetzt. Begründen kann man dies im Rahmen der Diffussion auf
fraktalen Gittern der Perkolationstheorie [15][3].
Für den Exponenten wurde hier bewußt der Buchstabe 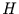 gewählt, da dieses
gewählt, da dieses
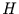 identisch mit dem
identisch mit dem 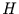 aus Abschnitt 5.3 ist
(s. [10]).
Ein Brownsches Rauschen erkennt man dann experimentell daran, daß
aus Abschnitt 5.3 ist
(s. [10]).
Ein Brownsches Rauschen erkennt man dann experimentell daran, daß
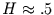 beobachtet wird. Für rosa Rauschen ist
beobachtet wird. Für rosa Rauschen ist 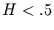 und für
schwarzes Rauschen gilt
und für
schwarzes Rauschen gilt 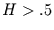 .
Für jede zu analysierende Zeitreihe kann nach Gleichung (34)
ein
.
Für jede zu analysierende Zeitreihe kann nach Gleichung (34)
ein 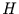 berechnet werden. Aber nur falls
berechnet werden. Aber nur falls 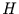 signifikant größer ist als
0 trägt es Information. Wegen Gleichung (26) kann mit Hilfe der
Strukturfunktion nur über fraktionell integrierte Prozesse mit
signifikant größer ist als
0 trägt es Information. Wegen Gleichung (26) kann mit Hilfe der
Strukturfunktion nur über fraktionell integrierte Prozesse mit 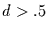 etwas ausgesagt werden.
Um auch Prozesse mit langem Gedächtnis und
etwas ausgesagt werden.
Um auch Prozesse mit langem Gedächtnis und
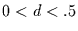 analysieren zu können, integriert man
die zu untersuchende
Zeitreihe, bevor man dann die Strukturfunktion der
integrierten Reihe
weiter untersucht. Man führt also die Operation
analysieren zu können, integriert man
die zu untersuchende
Zeitreihe, bevor man dann die Strukturfunktion der
integrierten Reihe
weiter untersucht. Man führt also die Operation
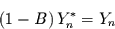 |
(35) |
d.h.
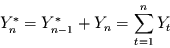 |
(36) |
durch, was gleichbedeutend damit ist, daß man einen
eindimensionalen Zufallswanderer die Werte der Zeitreihe 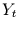 als Zufallsrauschen
übergibt.4
Für die integrierte Reihe folgt dann
ein Integrationsgrad
als Zufallsrauschen
übergibt.4
Für die integrierte Reihe folgt dann
ein Integrationsgrad 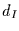 von
von
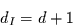 |
(37) |
und demnach auch
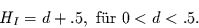 |
(38) |
Die Strukturfunktion der integrierten Zeitreihe ist demnach
für 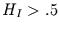 ein sinnvolles Maß für
ein sinnvolles Maß für 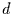 .
Eine Interpretation der Strukturfunktion der integrierten Zeitreihe
folgt, indem man die Summen der Integration in die Strukturfunktion einsetzt.
Man erhält dann aus Gleichung (36) und (30)
.
Eine Interpretation der Strukturfunktion der integrierten Zeitreihe
folgt, indem man die Summen der Integration in die Strukturfunktion einsetzt.
Man erhält dann aus Gleichung (36) und (30)
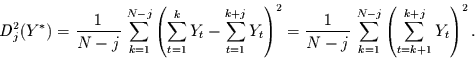 |
(39) |
Man kann dann die integrierte Funktion 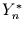 für jeden Startwert
für jeden Startwert
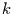 und jede Integrationslänge
und jede Integrationslänge 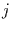 definieren und damit schreiben
definieren und damit schreiben
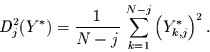 |
(40) |
Damit ist
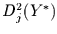 nichts anderes als die Varianz der Realisationen
der Integrationen der Länge
nichts anderes als die Varianz der Realisationen
der Integrationen der Länge 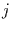 .
Für die integrierte Zeitreihe kann man nun wieder nach einem Skalengesetz
der Art
.
Für die integrierte Zeitreihe kann man nun wieder nach einem Skalengesetz
der Art
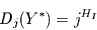 |
(41) |
mit dem Exponenten 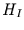 suchen.
Als Beispiel für die Anwendung der Strukturfunktion der integrierten Reihe
kann man für das integrierte weiße Rauschen (also die
eindimensionale Brownsche Bewegung) leicht folgendes ausrechnen:
suchen.
Als Beispiel für die Anwendung der Strukturfunktion der integrierten Reihe
kann man für das integrierte weiße Rauschen (also die
eindimensionale Brownsche Bewegung) leicht folgendes ausrechnen:
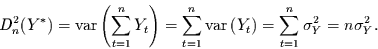 |
(42) |
Man sieht das bekannte Ergebnis5,
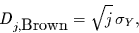 |
(43) |
daß die Standardabweichung bei der
Brownschen Bewegung mit der Wurzel der Zeit zunimmt, und proportional der
Standardabweichung der einzelnen Zufallsstöße ist.
Damit ist 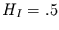 für Gaußsches weißes Rauschen.
Die Berechnung von
für Gaußsches weißes Rauschen.
Die Berechnung von 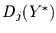 der integrierten Zeitreihe
wird z.T. auch Fluktuationsanalyse genannt
([8]). Die integrierte Zeitreihe selbst heißt
zuweilen Profil der Zeitreihe ([18]).
der integrierten Zeitreihe
wird z.T. auch Fluktuationsanalyse genannt
([8]). Die integrierte Zeitreihe selbst heißt
zuweilen Profil der Zeitreihe ([18]).



Nächste Seite: Der Hurst-Exponent
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Das Spektrum
Inhalt
ich
2000-01-25
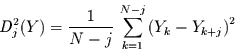
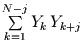 nicht unbedingt schnell gegen null.
Darüberhinaus kann für instationäre Prozesse
nicht unbedingt schnell gegen null.
Darüberhinaus kann für instationäre Prozesse
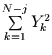 nicht gleich
nicht gleich
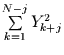 gesetzt werden.
Aus der Tatsache, daß die Strukturfunktion dann
immer weiter divergiert, kann man
den instationären Prozeß mit langem Gedächtnis (d.h.
gesetzt werden.
Aus der Tatsache, daß die Strukturfunktion dann
immer weiter divergiert, kann man
den instationären Prozeß mit langem Gedächtnis (d.h.