



Nächste Seite: Maße für Prozesse mit
Aufwärts: Die Farben des Rauschens
Vorherige Seite: Farben des FIWN-Rauschens
Inhalt
Exakte Definition des Brownschen Rauschens
Die gewöhnliche klassische Brownsche Bewegung hat viele Namen.
Unter ihnen sind Wiener-Funktion, Bachelier-Funktion,
Bachelier-Wiener-Lévy-Funktion und Wiener-Prozeß. Mandelbrot
[10] unterscheidet verschiedene Typen von Brown-Funktionen,
von denen sein Typ Brown-Funktion vom Typ Gerade-Gerade gerade das
ist, was man im klassischen Sinn unter Brownscher Bewegung versteht. Für
diese Brownsche Bewegung gilt unter den Bedingungen
- a)
- die Zeitvariable
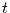 ist reell,
ist reell,
- b)
- die Raumvariable
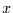 ist reell,
ist reell,
- c)
- der Parameter
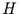 besitzt den Wert
besitzt den Wert 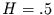 und
und
- d)
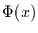 ist die Verteilungsfunktion der Standardnormalverteilung
ist die Verteilungsfunktion der Standardnormalverteilung
die Definition:
Die Brown-Funktion ist eine zufällige Funktion, für die
![\begin{displaymath}
Pr([B(t+\Delta t)-B(t)]/\vert\Delta t\vert^{H}< x) = \Phi(x)
\end{displaymath}](img103.gif) |
(25) |
für alle 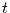 und
und 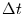 gilt.
gilt.
Für 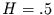 , wie in der Definition benutzt, erhält man die klassische
Brownsche Bewegung. Der Definition nach sind die Zuwächse dann Gaußsches
weißes Rauschen.
Dem Parameter
, wie in der Definition benutzt, erhält man die klassische
Brownsche Bewegung. Der Definition nach sind die Zuwächse dann Gaußsches
weißes Rauschen.
Dem Parameter 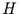 kann ein anderer Wert zwischen 0 und 1 zugeordnet werden.
Man hat es dann mit einer verallgemeinerten Brownschen Bewegung zu tun, die
als fraktionelle Brownsche Bewegung bezeichnet wird.
Der Bestimmung des Parameters
kann ein anderer Wert zwischen 0 und 1 zugeordnet werden.
Man hat es dann mit einer verallgemeinerten Brownschen Bewegung zu tun, die
als fraktionelle Brownsche Bewegung bezeichnet wird.
Der Bestimmung des Parameters 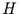 kommt in der Analyse von instationären
Zeitreihen
aus Prozessen mit langem Gedächtnis große Bedeutung zu.
Dies liegt
insbesondere daran, daß zwischen dem
kommt in der Analyse von instationären
Zeitreihen
aus Prozessen mit langem Gedächtnis große Bedeutung zu.
Dies liegt
insbesondere daran, daß zwischen dem 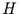 aus Gleichung (25)
und dem Grad der fraktionellen Integration
aus Gleichung (25)
und dem Grad der fraktionellen Integration 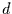 für instationäre
Prozesse der wichtige Zusammenhang
für instationäre
Prozesse der wichtige Zusammenhang
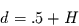 |
(26) |
für 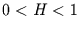 gilt. Damit kann
gilt. Damit kann 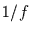 - bis
- bis 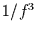 -Rauschen charakterisiert
werden. Darüber hinausgehende Fälle findet man in [10].
-Rauschen charakterisiert
werden. Darüber hinausgehende Fälle findet man in [10].




Nächste Seite: Maße für Prozesse mit
Aufwärts: Die Farben des Rauschens
Vorherige Seite: Farben des FIWN-Rauschens
Inhalt
ich
2000-01-25