



Nächste Seite: Cantor-Staub-Methode
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Die Strukturfunktion
Inhalt
``Hursts Name ist sicher auf immer in die Wissenschaft eingegangen,
und zwar wegen
einer von ihm erdachten statistischen Methode, mit der er ein bedeutendes
empirisches Gesetz über Langzeitabhängigkeiten in der Geophysik entdeckte``.
So ehrt B. Mandelbrot (s. [10])
den Hydrologen Harold Edwin Hurst (1900-1978).
Der nach ihm
benannte Exponent gibt eine
skalierte Spannweite einer Zeitreihe an. Er ist ein allgemeines Maß für
das Gedächtnis eines Prozesses, daß insbesondere auch bei
schwarzem Rauschen, daß B. Mandelbrot [10]
deshalb Hurst-Rauschen nannte, gut
anwendbar ist. Bei solchen instationären Rauschen können die Methoden,
die auf die Stationarität, d.h. insbesondere die Existenz von Momenten
zweiter Ordnung angewiesen sind, nicht mehr vertrauenswürdig eingesetzt
werden. Der Hurst-Exponent ist somit ein robustes Maß, das
für instationäre Prozesse, d.h. ab 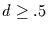 interessant ist.
Im Gegensatz zur Strukturfunktion, bei der die Verschiebung in Abhängigkeit
von der vergehenden Zeit untersucht wird, wird hier eine korrigierte
Reichweite (adjusted range)
interessant ist.
Im Gegensatz zur Strukturfunktion, bei der die Verschiebung in Abhängigkeit
von der vergehenden Zeit untersucht wird, wird hier eine korrigierte
Reichweite (adjusted range) 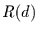 in Abhängigkeit von der Zeit untersucht.
Dazu werden wieder integrierte Zeitreihensegmente
in Abhängigkeit von der Zeit untersucht.
Dazu werden wieder integrierte Zeitreihensegmente
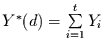 gebildet. Es gilt dann die
Definitionsbeziehung
gebildet. Es gilt dann die
Definitionsbeziehung
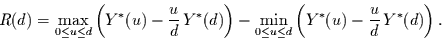 |
(44) |
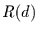 mißt somit die
maximale Abweichung vom linearen Trend der integrierten
Zeitreihe. Diese wird dann mit der Stichprobenstandardabweichung
mißt somit die
maximale Abweichung vom linearen Trend der integrierten
Zeitreihe. Diese wird dann mit der Stichprobenstandardabweichung
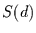 normiert zur sogenannten R/S-Statistik, für die bei Prozessen mit
langem Gedächtnis gilt
normiert zur sogenannten R/S-Statistik, für die bei Prozessen mit
langem Gedächtnis gilt
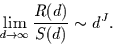 |
(45) |
Man kann weiterhin zeigen, daß 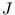 für rosa, Brownsches und schwarzes Rauschen
gleich
für rosa, Brownsches und schwarzes Rauschen
gleich 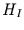 ist. Damit ist der
Hurst-Exponent ein robusterer Schätzer für
ist. Damit ist der
Hurst-Exponent ein robusterer Schätzer für 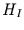 .
Für weißes Rauschen (und
Rauschen aus Prozessen mit kurzem Gedächtnis, d.h.
.
Für weißes Rauschen (und
Rauschen aus Prozessen mit kurzem Gedächtnis, d.h. 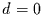 )
gilt
)
gilt 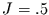 , während
für stationäres Rauschen mit
, während
für stationäres Rauschen mit 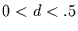 der Wertebereich
der Wertebereich 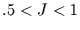 ,
für instationäres Rauschen mit
,
für instationäres Rauschen mit 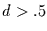
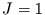 zu erwarten ist.
Es ist im letzten Fall sinnvoll die differenzierte Reihe zu untersuchen,
d.h. den fraktionalen Charakter der Zuwächse.
Der Wasserstand des Rheins
bei Basel zwischen 1808 und 1966 ergibt
zu erwarten ist.
Es ist im letzten Fall sinnvoll die differenzierte Reihe zu untersuchen,
d.h. den fraktionalen Charakter der Zuwächse.
Der Wasserstand des Rheins
bei Basel zwischen 1808 und 1966 ergibt
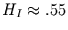 , während die
Nilwasserstände von 622 bis 1469 ungefähr
, während die
Nilwasserstände von 622 bis 1469 ungefähr
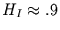 ergeben
(s. [15]). Schlittgen und Streitberg ([14])
geben ein
ergeben
(s. [15]). Schlittgen und Streitberg ([14])
geben ein
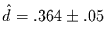 aus der Analyse des Spektrums.
Beide Ergebnisse stimmen sehr gut überein.
aus der Analyse des Spektrums.
Beide Ergebnisse stimmen sehr gut überein.




Nächste Seite: Cantor-Staub-Methode
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Die Strukturfunktion
Inhalt
ich
2000-01-25
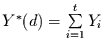 gebildet. Es gilt dann die
Definitionsbeziehung
gebildet. Es gilt dann die
Definitionsbeziehung