



Nächste Seite: Zusammenhänge zwischen den Maßen
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Der Hurst-Exponent
Inhalt
Eine Zeitreihe, für die
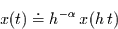 |
(46) |
gilt, heißt
skaleninvariant6. Dieser Zusammenhang bedeutet, daß ein
vergrößerter Ausschnitt der Zeitreihe statistisch identisch ist
mit der ursprünglichen Zeitreihe.
Für die Zeitreihenanalyse bedeutet das, daß Beobachtungen statistischer
Eigenschaften auf einer
bestimmten Zeitskala durch Skalenzusammenhänge dazu genutzt werden
können, etwas über die statistischen Eigenschaften auf nicht beobachteten
Skalen auszusagen.
Der Begriff statistisch identisch soll
durch das Zeichen 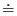 repräsentiert sein. Nun kann man sich
verallgemeinernd vorstellen, daß eine solche Skaleninvarianz bis zu so kleinen
Skalen gilt, daß man
repräsentiert sein. Nun kann man sich
verallgemeinernd vorstellen, daß eine solche Skaleninvarianz bis zu so kleinen
Skalen gilt, daß man 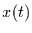 als kontinuierliche Funktion in der Zeit
interpretieren darf und trotzdem noch auf allen Skalen Gleichung
(46) gilt. Dann kann die kontinuierliche Funktion in der Zeit eine
fraktale Dimension haben. Diese Dimension muß zwischen eins (der Linie)
und 2 (der Fläche) liegen. Sie ist nach Mandelbrot [10]
gegeben durch
als kontinuierliche Funktion in der Zeit
interpretieren darf und trotzdem noch auf allen Skalen Gleichung
(46) gilt. Dann kann die kontinuierliche Funktion in der Zeit eine
fraktale Dimension haben. Diese Dimension muß zwischen eins (der Linie)
und 2 (der Fläche) liegen. Sie ist nach Mandelbrot [10]
gegeben durch
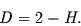 |
(47) |
Je kleiner 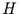 also ist, d.h. je stärker die Funktion dazu neigt, auf und
ab zuschwingen, desto mehr Raum füllt sie aus.
Eine solche Funktion wird auch beliebige Niveaulinien öfter schneiden, als
eine Funktion mit größerem
also ist, d.h. je stärker die Funktion dazu neigt, auf und
ab zuschwingen, desto mehr Raum füllt sie aus.
Eine solche Funktion wird auch beliebige Niveaulinien öfter schneiden, als
eine Funktion mit größerem 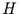 . Für die Dimension einer Niveaumenge
gilt dann
. Für die Dimension einer Niveaumenge
gilt dann
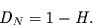 |
(48) |
Für 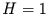 ist die Zeitreihe keine diskrete Darstellung eines Fraktals,
und die kontinuierliche Zeitfunktion ist eindimensional,
während sich die Niveaumenge auf Punkte reduziert.
Die Dimension einer Niveaumenge einer skaleninvarianten Zeitreihe kann man
wiederum über einen Box-Counting-Algorithmus berechnen, der im eindimensionalen
Fall einer Niveaulinie eine besonders einfache Form annimmt und in der
Arbeit von Mazzarella [11] als Cantor-Staub-Methode
(Cantor Dust Method) bezeichnet wird. Bei der Anwendung dieser Methode
wählt man zunächst eine Niveauline aus (z.B. das
ist die Zeitreihe keine diskrete Darstellung eines Fraktals,
und die kontinuierliche Zeitfunktion ist eindimensional,
während sich die Niveaumenge auf Punkte reduziert.
Die Dimension einer Niveaumenge einer skaleninvarianten Zeitreihe kann man
wiederum über einen Box-Counting-Algorithmus berechnen, der im eindimensionalen
Fall einer Niveaulinie eine besonders einfache Form annimmt und in der
Arbeit von Mazzarella [11] als Cantor-Staub-Methode
(Cantor Dust Method) bezeichnet wird. Bei der Anwendung dieser Methode
wählt man zunächst eine Niveauline aus (z.B. das 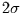 -Niveau oder
den Mittelwert). Dann
teilt man die gesammte Zeitreihe in Segmente der Länge
-Niveau oder
den Mittelwert). Dann
teilt man die gesammte Zeitreihe in Segmente der Länge 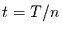 für
für
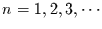 ein, und berechnet jeweils den Anteil
ein, und berechnet jeweils den Anteil 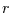 der Segmente, in denen
die Zeitreihe die Niveaulinie kreuzt.
Es gilt dann das Skalengesetz
der Segmente, in denen
die Zeitreihe die Niveaulinie kreuzt.
Es gilt dann das Skalengesetz
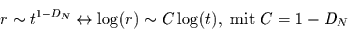 |
(49) |
mit dem 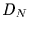 sehr einfach berechnet werden kann. Falls die Zeitreihe nicht
skaleninvariant ist, ist
sehr einfach berechnet werden kann. Falls die Zeitreihe nicht
skaleninvariant ist, ist 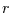 unabhängig von der Partitionierung,
d.h.
unabhängig von der Partitionierung,
d.h. 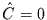 . Andernfalls ist
. Andernfalls ist 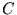 ein Schätzer für
ein Schätzer für 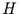 .
.




Nächste Seite: Zusammenhänge zwischen den Maßen
Aufwärts: Maße für Prozesse mit
Vorherige Seite: Der Hurst-Exponent
Inhalt
ich
2000-01-25