



Nächste Seite: Autokorrelationsfunktion
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Analyse von Beobachtungszeitreihen
Inhalt
Hier sollen nun drei Beobachtungszeitreihen analysiert werden. Dies sind
einerseits zwei meteorologische Meßreihen und andererseits eine
dendrologische Beobachtungsreihe.
Die
erste Reihe (Temp) umfaßt 2000 Monatsmitteltemperaturen von
Genf bis Dezember 1990. Die zweite Reihe umfaßt 1980 Werte der monatlichen
Niederschlagssummen (Rain) bis
1990 in Genf und die dritte Reihe umfaßt
Jahrringbreiten von Eichen aus Süddeutschland (Baum)
für die letzten 2000 Jahre bis 1985.
Die letzte Reihe wurde dankenswerter Weise vom Deutschen
Archäologischen Institut (DAI) [6] zur Verfügung gestellt.
Die ersten beiden Reihen werden vom Jahresgang befreit, indem alle
signifikanten Terme der folgenden Gleichung abgezogen werden:
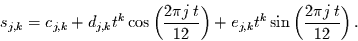 |
(59) |
Für 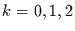 und
und 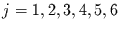 werden dann alle signifikanten Komponenten
des Jahresgangs und deren monotone langsame Veränderungen eliminiert.
Zunächst wird die Stationarität aller drei Zeitreihen getestet. Keine der
Zeitreihen ist mittelwertstationär (Ablehnungswahrscheinlichkeiten
werden dann alle signifikanten Komponenten
des Jahresgangs und deren monotone langsame Veränderungen eliminiert.
Zunächst wird die Stationarität aller drei Zeitreihen getestet. Keine der
Zeitreihen ist mittelwertstationär (Ablehnungswahrscheinlichkeiten
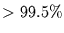 ). Die Reihe Temp ist darüberhinaus mit 93%
Wahrscheinlichkeit nicht varianzstationär. Keines der untersuchten Momente
der Reihe Baum ist stationär.
). Die Reihe Temp ist darüberhinaus mit 93%
Wahrscheinlichkeit nicht varianzstationär. Keines der untersuchten Momente
der Reihe Baum ist stationär.
ich
2000-01-25