



Nächste Seite: Spektrum
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Die Beobachtungsdaten
Inhalt
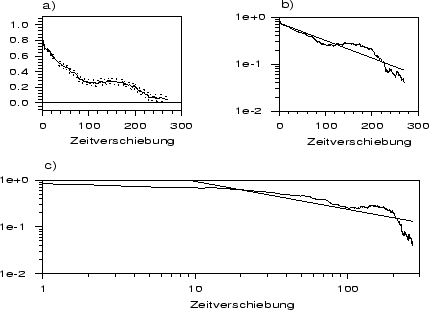
Die Autokorrelationsfunktion der Zeitreihe Temp ist in Abbildung
9 in den drei Darstellungsformen Lin-Lin, Log-Lin und Log-Log
wiedergegeben.
Abbildung 9:
Autokorrelationsfunktion der Reihe Temp in (a) Lin-Lin-Darstellung
(inkl. 90% Konfidenzintervall),
(b) Log-Lin-Darstellung und (c) Log-Log-Darstellung.
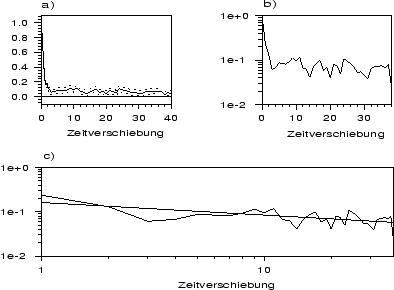 |
Wie man in Teil a) der Abbildung
sieht, fällt sie sehr schnell auf einen sehr geringen Betrag (ca. .1)
ab, auf dem sie dann recht konstant zu bleiben scheint. Bis zu einer
Zeitverschiebung von 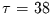 Monaten ist die geschätzte
Autokorrelationsfunktion des die Zeitreihe erzeugenden Prozesses
mit 95% Wahrscheinlichkeit größer null. Der Korrelationskoeffizient
der Zeitreihe erreicht den Wert null erstmals bei einer Zeitverschiebung von
138 Monaten. Der erste Wert, von dem man mit 95% Wahrscheinlichkeit sagen
kann, daß er unter Null liegt, tritt bei 662 Monaten Zeitverschiebung auf.
Wir können also davon ausgehen, daß die Autokorrelationsfunktion mit
sehr großer Wahrscheinlichkeit über einen sehr langen Zeitraum größer
null ist. In Teil b) von Abbildung 9
ist die Autokorrelationsfunktion
für die ersten 38 Verschiebungen in der Log-Lin-Darstellung angegeben. Man
sieht keinen
linearen Zusammenhang, wie man ihn bei einem AR(1)-Prozeß erwarten
würde. Eine optimal angepaßte Gerade erklärt 8% der Varianz bei
einer Steigung von
Monaten ist die geschätzte
Autokorrelationsfunktion des die Zeitreihe erzeugenden Prozesses
mit 95% Wahrscheinlichkeit größer null. Der Korrelationskoeffizient
der Zeitreihe erreicht den Wert null erstmals bei einer Zeitverschiebung von
138 Monaten. Der erste Wert, von dem man mit 95% Wahrscheinlichkeit sagen
kann, daß er unter Null liegt, tritt bei 662 Monaten Zeitverschiebung auf.
Wir können also davon ausgehen, daß die Autokorrelationsfunktion mit
sehr großer Wahrscheinlichkeit über einen sehr langen Zeitraum größer
null ist. In Teil b) von Abbildung 9
ist die Autokorrelationsfunktion
für die ersten 38 Verschiebungen in der Log-Lin-Darstellung angegeben. Man
sieht keinen
linearen Zusammenhang, wie man ihn bei einem AR(1)-Prozeß erwarten
würde. Eine optimal angepaßte Gerade erklärt 8% der Varianz bei
einer Steigung von 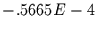 . Der Schätzwert des zugeordneten
AR(1)-Koeffizienten ist dann
. Der Schätzwert des zugeordneten
AR(1)-Koeffizienten ist dann
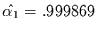 . Das wiederum
ist dem Wert
. Das wiederum
ist dem Wert
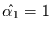 , der Brownschen Bewegung sehr nahe. Zu
dieser Anpassung passen die Werte der Verschiebung 1 und 2 nicht. Dies ist
zunächst rein hypothetisch damit erklärbar, daß die
Autokorrelationsfunktion eines ARMA-Prozesses
der Ordnung (p,q) ab einer Zeitverschiebung
, der Brownschen Bewegung sehr nahe. Zu
dieser Anpassung passen die Werte der Verschiebung 1 und 2 nicht. Dies ist
zunächst rein hypothetisch damit erklärbar, daß die
Autokorrelationsfunktion eines ARMA-Prozesses
der Ordnung (p,q) ab einer Zeitverschiebung
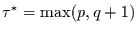 [14], nur noch durch den
autoregressiven Anteil bestimmt ist. Dann ist entweder
[14], nur noch durch den
autoregressiven Anteil bestimmt ist. Dann ist entweder 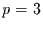 oder
oder 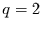 zu
erwarten. Setzt man also voraus, daß sich der Prozeß
für Zeitverschiebungen größer 2 nicht mehr von einem AR(1)-Prozeß
unterscheidet, so folgt daß er eine Realisierung eines ARMA(1,2)-Prozesses
ist.
Wir könnten es hier demnach mit einem Prozeß mit langem
Gedächtnis zu tun haben (
zu
erwarten. Setzt man also voraus, daß sich der Prozeß
für Zeitverschiebungen größer 2 nicht mehr von einem AR(1)-Prozeß
unterscheidet, so folgt daß er eine Realisierung eines ARMA(1,2)-Prozesses
ist.
Wir könnten es hier demnach mit einem Prozeß mit langem
Gedächtnis zu tun haben (
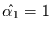 ), der für kleine Zeitschritte
durch den MA(2)-Anteil verdeckt ist.
Diese plausible
Hypothese könnte an dieser Stelle weiter getestet werden. Stattdessen soll
sie nur als Anregung dienen, denn in
Teil c) der Abbildung sieht man, daß eine Gerade in der
Log-Log-Darstellung die Autokorrelationsfunktion
ebenfalls recht gut wiedergibt. Die Steigung
der Geraden ist
), der für kleine Zeitschritte
durch den MA(2)-Anteil verdeckt ist.
Diese plausible
Hypothese könnte an dieser Stelle weiter getestet werden. Stattdessen soll
sie nur als Anregung dienen, denn in
Teil c) der Abbildung sieht man, daß eine Gerade in der
Log-Log-Darstellung die Autokorrelationsfunktion
ebenfalls recht gut wiedergibt. Die Steigung
der Geraden ist 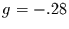 und erklärt 10% der Varianz der ersten 38
Autokorrelationskoeffizienten. Daraus kann man vermuten, daß die
Temperaturzeitreihe der Station Genf durch einen fraktionell differenzierten
White-Noise-Prozeß mit
und erklärt 10% der Varianz der ersten 38
Autokorrelationskoeffizienten. Daraus kann man vermuten, daß die
Temperaturzeitreihe der Station Genf durch einen fraktionell differenzierten
White-Noise-Prozeß mit
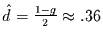 dargestellt werden kann. Es gelingt demnach nicht, anhand der
Autokorrelationsfunktion zwischen einem Prozeß mit langem Gedächtnis und
dargestellt werden kann. Es gelingt demnach nicht, anhand der
Autokorrelationsfunktion zwischen einem Prozeß mit langem Gedächtnis und
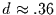 und einem anderen Prozeß mit langem Gedächtnis
9
zu unterscheiden.
Die Autokorrelationsfunktion der Reihe Rain ist ab Zeitverschiebungen
von 1 nicht mehr mit 95% Wahrscheinlichkeit von null zu unterscheiden.
Daraus kann geschlossen werden, daß sie nicht aus einem
ARMA-Prozeß stammt. Sie scheint kein Gedächtnis zu haben.
Die Autokorrelationsfunktion der Reihe Baum ist in Abbildung
10 in den bekannten drei Darstellungsformen wiedergegeben.
Man sieht zunächst in Abbildung 10a, daß die Autokorrelationsfunktion
nur langsam gegen null geht. Dabei ist der Wert bei der Verschiebung 271
der erste nicht mehr signifikant von null unterscheidbare Wert. Erst bei
einer Verschiebung von 805 wird die Autokorrelation kleiner 0. In der
Log-Lin-Darstellung
in Abbildung 10b sieht man einen guten linearen
Zusammenhang. Bei einer erklärten Varianz von 88% und einer Steigung von
und einem anderen Prozeß mit langem Gedächtnis
9
zu unterscheiden.
Die Autokorrelationsfunktion der Reihe Rain ist ab Zeitverschiebungen
von 1 nicht mehr mit 95% Wahrscheinlichkeit von null zu unterscheiden.
Daraus kann geschlossen werden, daß sie nicht aus einem
ARMA-Prozeß stammt. Sie scheint kein Gedächtnis zu haben.
Die Autokorrelationsfunktion der Reihe Baum ist in Abbildung
10 in den bekannten drei Darstellungsformen wiedergegeben.
Man sieht zunächst in Abbildung 10a, daß die Autokorrelationsfunktion
nur langsam gegen null geht. Dabei ist der Wert bei der Verschiebung 271
der erste nicht mehr signifikant von null unterscheidbare Wert. Erst bei
einer Verschiebung von 805 wird die Autokorrelation kleiner 0. In der
Log-Lin-Darstellung
in Abbildung 10b sieht man einen guten linearen
Zusammenhang. Bei einer erklärten Varianz von 88% und einer Steigung von
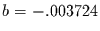 liegt es nahe, daß die Reihe Baum aus einem AR(1)-Prozeß mit
dem geschätzten Koeffizienten
liegt es nahe, daß die Reihe Baum aus einem AR(1)-Prozeß mit
dem geschätzten Koeffizienten
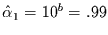 stammt. Dies
wiederum liegt sehr nahe an einem Prozeß mit langem Gedächtnis, denn für
stammt. Dies
wiederum liegt sehr nahe an einem Prozeß mit langem Gedächtnis, denn für
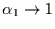 geht das stationäre AR(1)-Rauschen in das
instationäre Brownsche Rauschen über.
Letzten Endes betrachten wir die
in Abbildung 10c
gegebene Log-Log-Darstellung der Autokorrelationsfunktion.
Auch hier scheint ein linearer Zusammenhang sichtbar zu sein. Für die ersten
zwanzig Zeitverschiebungen folgt eine Steigung von
geht das stationäre AR(1)-Rauschen in das
instationäre Brownsche Rauschen über.
Letzten Endes betrachten wir die
in Abbildung 10c
gegebene Log-Log-Darstellung der Autokorrelationsfunktion.
Auch hier scheint ein linearer Zusammenhang sichtbar zu sein. Für die ersten
zwanzig Zeitverschiebungen folgt eine Steigung von 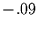 bei einer erklärten
Varianz von 96%. Betrachtet man hingegen die ersten 270 Zeitverschiebungen,
so erklärt ein linearer Zusammenhang nur noch 65% der Varianz bei einer
Steigung von -.59. Hieraus scheint man demnach keine Aussagen über ein
mögliches langes Gedächtnis ableiten zu können.
bei einer erklärten
Varianz von 96%. Betrachtet man hingegen die ersten 270 Zeitverschiebungen,
so erklärt ein linearer Zusammenhang nur noch 65% der Varianz bei einer
Steigung von -.59. Hieraus scheint man demnach keine Aussagen über ein
mögliches langes Gedächtnis ableiten zu können.
Abbildung 10:
Autokorrelationsfunktion der Reihe Baum in (a) Lin-Lin-Darstellung
(inkl. 90% Konfidenzintervall),
(b) Log-Lin-Darstellung und (c) Log-Log-Darstellung.
 |




Nächste Seite: Spektrum
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Die Beobachtungsdaten
Inhalt
ich
2000-01-25


