Nächste Seite: Strukturfunktion
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Autokorrelationsfunktion
Inhalt
Für alle drei Zeitreihen wurde das Spektrum berechnet.
Der Kolmogoroff-Smirnoff-Test und der Anderson-Darling-Test lehnen die
Hypothese, daß die Reihen Temp und Baum
aus einem White-Noise-Prozeß stammen mit
99% Wahrscheinlichkeit ab. Die Reihe Rain kann nur auf dem 95%
Niveau vom weißen Rauschen unterschieden werden.
Die drei
Spektren der drei Zeitreihen
sind zusammen mit einer optimalen linearen Anpassung und
dem Spektrum des optimal angepaßten AR(1)-Prozesses in Abbildung
11 als Log-Log-Darstellung für Frequenzen kleiner als
.1 der Zeitschrittlänge gegeben. Da der Autokorrelationskoeffizient
zur Verschiebung 1 der Reihe Rain nicht mit 95% Sicherheit von
null unterschieden werden kann, wird dieser Reihe kein optimal
angepaßtes AR(1)-Spektrum zugeordnet. Die Spektren der anderen beiden Reihen
werden durch das zugeordnete AR(1)-Spektrum nicht gut wiedergegeben.
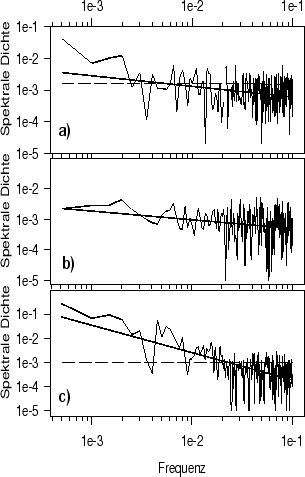
Abbildung:
Spektren von Zeitreihen mit jeweils ca. 2000 Werten aus
(a) Monatsmitteltemperaturen von Genf, (b) monatliche
Niederschlagssummen von Genf und (c)
Jahrringbreiten von Eichen in Süddeutschland
in Log-Log-Darstellung. Die Geraden sind optimal angepaßt.
Die unterbrochenen Linien entsprechen optimal
angepaßten AR(1)-Prozessen.
 |
Die Steigung 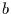 der in der Log-Log-Darstellung optimal angepaßten Geraden, wird nun als
Schätzer für den Exponenten
der in der Log-Log-Darstellung optimal angepaßten Geraden, wird nun als
Schätzer für den Exponenten 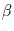 eines
eines 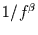 -Spektrums
verwendet. Man erhält dann
-Spektrums
verwendet. Man erhält dann
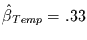 , mit einer
erklärten Varianz von 7%,
, mit einer
erklärten Varianz von 7%,
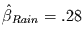 , mit einer erklärten
Varianz von 5% und
, mit einer erklärten
Varianz von 5% und
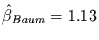 , mit einer erklärten
Varianz von 37%. Dabei ist zu beachten, daß Spektralschätzer nicht
Gauß-verteilt sondern asymptotisch exponentiell verteilt sind, so daß
die Anpassung einer optimalen Geraden statistisch nicht ganz sauber ist
10.
Würde man die Spektren erst glätten und dann die Geraden anpassen, so
würde man erstens statistisch sauberer sein (geglättete Spektren sind
asymptotisch Gauß-verteilt) und würde zweitens wegen der geringeren
Varianz des geglätteten Spektrums, die Steigung der Geraden besser
schätzen. Andererseits zeigt ein Blick auf Abbildung 11, daß
dies keinen wesentlichen Einfluß auf die Steigung der angepaßten Gerade
hätte. Aus den Steigungen der Geraden würde man demnach schätzen
, mit einer erklärten
Varianz von 37%. Dabei ist zu beachten, daß Spektralschätzer nicht
Gauß-verteilt sondern asymptotisch exponentiell verteilt sind, so daß
die Anpassung einer optimalen Geraden statistisch nicht ganz sauber ist
10.
Würde man die Spektren erst glätten und dann die Geraden anpassen, so
würde man erstens statistisch sauberer sein (geglättete Spektren sind
asymptotisch Gauß-verteilt) und würde zweitens wegen der geringeren
Varianz des geglätteten Spektrums, die Steigung der Geraden besser
schätzen. Andererseits zeigt ein Blick auf Abbildung 11, daß
dies keinen wesentlichen Einfluß auf die Steigung der angepaßten Gerade
hätte. Aus den Steigungen der Geraden würde man demnach schätzen
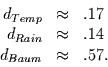 |
(60) |




Nächste Seite: Strukturfunktion
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Autokorrelationsfunktion
Inhalt
ich
2000-01-25