



Nächste Seite: Hurst-Exponent
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Spektrum
Inhalt
Für alle drei Beobachtungszeitreihen wird die Strukturfunktion berechnet.
Abbildung 12a, c, und e zeigt die Ergebnisse für die Reihen
Temp, Rain und Baum in der Log-Log-Darstellung.
Man sieht, daß die Strukturfunktion der Reihen
Temp und Rain in guter Näherung konstant sind, d.h. daß
für diese beiden Zeitreihen 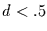 gilt.
Die angepaßten
Geraden zeigen eine unsignifikante Steigung im Bereich von
gilt.
Die angepaßten
Geraden zeigen eine unsignifikante Steigung im Bereich von
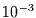 . Für die Reihe Baum hingegen liegt der Exponent zwischen
.1 und .18, und somit folgt als Schätzer für
. Für die Reihe Baum hingegen liegt der Exponent zwischen
.1 und .18, und somit folgt als Schätzer für
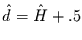 im Bereich des rosa Rauschens mit
im Bereich des rosa Rauschens mit
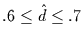 .
Auch die Strukturfunktion für die drei integrierten Reihen wurde berechnet.
Abbildung 13a, c, und e zeigt die Ergebnisse für die Reihen
Temp, Rain und Baum in der Log-Log-Darstellung.
Man sieht, daß die Annahme einer Geraden in der Log-Log-Darstellung sehr
gut erfüllt ist. Die Exponenten der integrierten
Strukturfunktion, die in den
Abbildungsteilen b), d) und f) dargestellt sind, liegen zwischen .52 und
.95, also alle im Bereich des rosa Rauschens. Dabei erscheint für die Reihe
Temp ein Exponent von ca. .74 gerechtfertigt, während der Exponent
bei der Reihe Rain nicht wesentlich von .5
abweicht. Für die Reihe Baum liegt der Exponent deutlich
über .9. Aus dem Wert des Exponenten der Strukturfunktion der
nichtintegrierten Zeitreihe erwartet man den Wert 1. Daraus folgt das einzig
Aussagbare
.
Auch die Strukturfunktion für die drei integrierten Reihen wurde berechnet.
Abbildung 13a, c, und e zeigt die Ergebnisse für die Reihen
Temp, Rain und Baum in der Log-Log-Darstellung.
Man sieht, daß die Annahme einer Geraden in der Log-Log-Darstellung sehr
gut erfüllt ist. Die Exponenten der integrierten
Strukturfunktion, die in den
Abbildungsteilen b), d) und f) dargestellt sind, liegen zwischen .52 und
.95, also alle im Bereich des rosa Rauschens. Dabei erscheint für die Reihe
Temp ein Exponent von ca. .74 gerechtfertigt, während der Exponent
bei der Reihe Rain nicht wesentlich von .5
abweicht. Für die Reihe Baum liegt der Exponent deutlich
über .9. Aus dem Wert des Exponenten der Strukturfunktion der
nichtintegrierten Zeitreihe erwartet man den Wert 1. Daraus folgt das einzig
Aussagbare
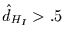 .
.
Abbildung:
Strukturfunktionen von Zeitreihen mit jeweils ca. 2000 Werten aus
(a) Monatsmitteltemperaturen von Genf, (c) monatliche
Niederschlagssummen von Genf und (e) Jahrringbreiten von Eichen
aus Süddeutschland in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für die Zeitreihe Temp (b), Rain (d) und Baum (f).
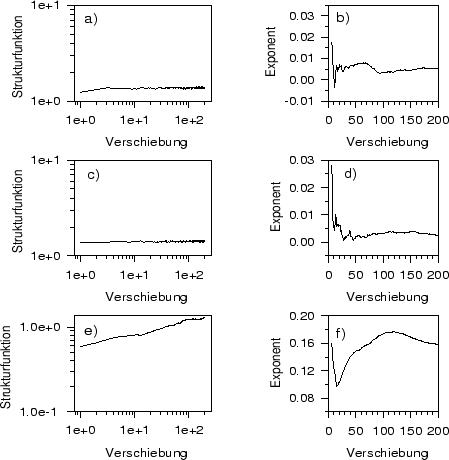 |
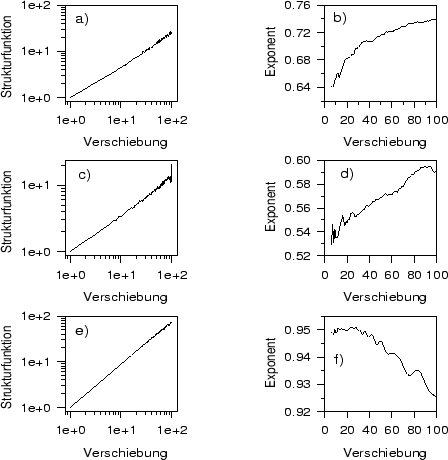
Abbildung:
Strukturfunktionen der integrierten Zeitreihen
Temp (a), Rain (c) und Baum (e)
in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für die Zeitreihe Temp (b), Rain (d) und Baum
(f).
 |




Nächste Seite: Hurst-Exponent
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Spektrum
Inhalt
ich
2000-01-25


