



Nächste Seite: Cantor-Dust-Methode
Aufwärts: Analyse von Beobachtungszeitreihen
Vorherige Seite: Strukturfunktion
Inhalt
Für alle drei Reihen und alle Zeitverschiebungen bis
zweihundert wird der Hurst-Exponent berechnet.
In Abbildung 14 ist sowohl 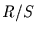 gegen die Zeitspanne
gegen die Zeitspanne 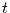 doppelt-logarithmisch dargestellt, als auch die Steigung der besten linearen
Anpassung.
Zwar sieht die Abhängigkeit
von
doppelt-logarithmisch dargestellt, als auch die Steigung der besten linearen
Anpassung.
Zwar sieht die Abhängigkeit
von 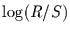 von der Zeitspanne
von der Zeitspanne 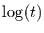 in allen drei Fällen linear
aus, jedoch nimmt sowohl im Fall der Reihe Temp, als auch im Fall der
Reihe Rain die Steigung kontinuierlich von Werten über .7 ab auf
etwa .64 im Fall der Reihe Temp und etwa .6 im Fall der Reihe
Rain.
Für die Reihe Baum konvergiert der Hurst-Exponent von unten
gegen
in allen drei Fällen linear
aus, jedoch nimmt sowohl im Fall der Reihe Temp, als auch im Fall der
Reihe Rain die Steigung kontinuierlich von Werten über .7 ab auf
etwa .64 im Fall der Reihe Temp und etwa .6 im Fall der Reihe
Rain.
Für die Reihe Baum konvergiert der Hurst-Exponent von unten
gegen 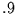 .
Da für
.
Da für 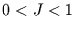 auch
auch
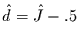 gilt, sind die Ergebnisse mit denen der
Strukturfunktion der integrierten Reihen vergleichbar.
gilt, sind die Ergebnisse mit denen der
Strukturfunktion der integrierten Reihen vergleichbar.
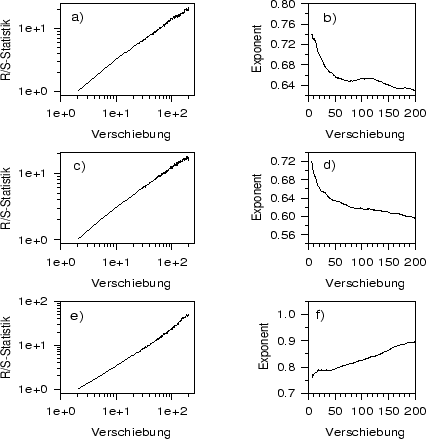
Abbildung:
Hurst-Exponenten der Zeitreihen
Temp (a), Rain (c) und Baum (e)
in Log-Log-Darstellung und
Steigung der bis zur angegebenen Verschiebung optimal angepaßten Geraden
für Temp (b), Rain (d) und Baum (f).
 |
ich
2000-01-25

