Nächste Seite: Fehlende räumliche Skala
Aufwärts: Fehlende Skalenlänge
Vorherige Seite: Fehlende Skalenlänge
Inhalt
Von Großmann [5] stammt eine sehr einfache Formulierung einer
Dynamik mit einem linearen und einem nichtlinearen Term.
Sie ist gegeben durch
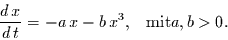 |
(61) |
Für den Fall 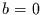 repräsentiert diese Gleichung einen linearen Speicher
mit einer Relaxationszeit
repräsentiert diese Gleichung einen linearen Speicher
mit einer Relaxationszeit 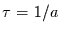 . Die zeitdiskrete Betrachtung dieses
Systems, wenn es mit Gaußschem weißen Rauschen angetrieben wird, führt
dann zu einem AR(1)-Prozeß und somit zu einer exponentiell abklingenden
Autokorrelationsfunktion.
Setzt man demhingegen
. Die zeitdiskrete Betrachtung dieses
Systems, wenn es mit Gaußschem weißen Rauschen angetrieben wird, führt
dann zu einem AR(1)-Prozeß und somit zu einer exponentiell abklingenden
Autokorrelationsfunktion.
Setzt man demhingegen 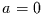 , so erhält man ein rein nichtlineares System,
mit der speziellen Lösung für einen gegebenen Anfangswert
, so erhält man ein rein nichtlineares System,
mit der speziellen Lösung für einen gegebenen Anfangswert 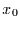
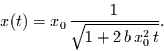 |
(62) |
Für nicht zu kleine Zeiten konvergiert diese Lösung gegen die
skaleninvariante Lösung
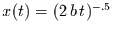 . Es gibt in diesem Fall
keine typische Zeitskala, wie es die Relaxationszeit im rein linearen Fall
war. Wird die Zeit um den Faktor
. Es gibt in diesem Fall
keine typische Zeitskala, wie es die Relaxationszeit im rein linearen Fall
war. Wird die Zeit um den Faktor 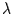 gedehnt, erhält man die gleiche
Lösung mit einer um
gedehnt, erhält man die gleiche
Lösung mit einer um 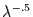 gestauchten Amplitude.
Leider ist es mir
nicht gelungen, die Autokorrelationsfunktion des mit Gaußschem weißen
Rauschen angetriebenen vollständigen Systems anzugeben. Jedoch wird die Lösung des
Anfangswertproblems für lange Zeiten immer vom exponentiellen Abklingen
dominiert, wenn der lineare Term nicht vernachlässigt wird. Es ist also
möglich, daß skaleninvarianten Verhaltens in der Autokorrelationsfunktion
sichtbar wird, obwohl jeder einzelne Anstoß für nicht zu kurze Zeiten
exponentiell abklingt.
Eine ausführlichere Diskussion von Gleichung (61) findet man z.B.
in [9].
gestauchten Amplitude.
Leider ist es mir
nicht gelungen, die Autokorrelationsfunktion des mit Gaußschem weißen
Rauschen angetriebenen vollständigen Systems anzugeben. Jedoch wird die Lösung des
Anfangswertproblems für lange Zeiten immer vom exponentiellen Abklingen
dominiert, wenn der lineare Term nicht vernachlässigt wird. Es ist also
möglich, daß skaleninvarianten Verhaltens in der Autokorrelationsfunktion
sichtbar wird, obwohl jeder einzelne Anstoß für nicht zu kurze Zeiten
exponentiell abklingt.
Eine ausführlichere Diskussion von Gleichung (61) findet man z.B.
in [9].




Nächste Seite: Fehlende räumliche Skala
Aufwärts: Fehlende Skalenlänge
Vorherige Seite: Fehlende Skalenlänge
Inhalt
ich
2000-01-25