

Nächste Seite: Über dieses Dokument ...
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Ergebnisse
Der Erwartungswert einer Zufallszeitreihe 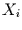 ist definiert als
ist definiert als
![\begin{displaymath}
E[X] = \sum\limits_{i=1}^{\infty}x_{i}\,p_{i}.
\end{displaymath}](img150.gif) |
(58) |
Dabei ist 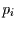 die Wahrscheinlichkeit dafür, zum Zeitpunkt
die Wahrscheinlichkeit dafür, zum Zeitpunkt 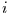 den
Wert
den
Wert 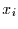 vorzufinden.
Man kann damit leicht zeigen, daß
vorzufinden.
Man kann damit leicht zeigen, daß
![\begin{displaymath}
E[a\,X] = a\,E[X]
\end{displaymath}](img154.gif) |
(59) |
ist, also insbesondere auch
![\begin{displaymath}
E\left[E[X]\,X\right] = E[X] \,E[X].
\end{displaymath}](img155.gif) |
(60) |
Falls eine Zufallszeitreihe stationär ist,
vereinfacht sich Glg. (58) zu
![\begin{displaymath}
E[X] =\lim\limits_{N\to\infty}\frac{1}{N} \sum\limits_{i=1}^{N}x_{i},
\end{displaymath}](img156.gif) |
(61) |
da die stationäre Wahrscheinlichkeitsverteilung dann durch die Realisationen
gegeben ist.
Der Mittelwert über 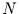 Werte einer beliebigen Zeitreihe
Werte einer beliebigen Zeitreihe 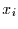 kann angegeben werden durch
kann angegeben werden durch
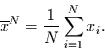 |
(62) |
Stammt die Zeitreihe nun aus einem stationären Rauschen, so
konvergiert dieser Ausdruck für große 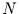 gegen den Erwartungswert des
Rauschens.
Für kleine Werte von
gegen den Erwartungswert des
Rauschens.
Für kleine Werte von 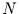 wird
wird
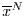 aber noch erheblichen
Schwankungen unterworfen sein können. Diese gilt es nun formal zu erfassen.
Dazu werden zunächst die Definitionen der Varianz
aber noch erheblichen
Schwankungen unterworfen sein können. Diese gilt es nun formal zu erfassen.
Dazu werden zunächst die Definitionen der Varianz ![$\mbox{var}[X]$](img159.gif) und
der Kovarianz
und
der Kovarianz ![$\mbox{cov}[X]$](img160.gif) gegeben und jeweils in für die Anwendung
sinnvolle Formen gebracht.
Die Varianz ist definiert als
gegeben und jeweils in für die Anwendung
sinnvolle Formen gebracht.
Die Varianz ist definiert als
![\begin{displaymath}
\mbox{var}[X] = E\left[(X-E[X])^{2}\right].
\end{displaymath}](img161.gif) |
(63) |
Daraus folgt mit den oben angegebenen Regeln für Erwartungswerte
![\begin{displaymath}
\mbox{var}[X] = E\left[X^{2}\right] - E[X]^{2}.
\end{displaymath}](img162.gif) |
(64) |
Mit der Definition der Varianz und den Regeln für Erwartungswerte kann
man zeigen, daß für jede reelle Zahl 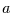 gilt
gilt
![\begin{displaymath}
\mbox{var}[a\,X] = a^{2}\,\mbox{var}[X].
\end{displaymath}](img163.gif) |
(65) |
Die Kovarianz ist definiert als
![\begin{displaymath}
\mbox{cov}[X_{i},X_{j}] = E\left[(X_{i}-E[X_{i}])\,(X_{j}-E[X_{j}])\right],
\end{displaymath}](img164.gif) |
(66) |
woraus mit den oben angegebenen Regeln für Erwartungswerte folgt
![\begin{displaymath}
\mbox{cov}[X_{i},X_{j}] = E\left[X_{i}\,X_{j}\right] - E\left[X_{i}\right]
E\left[X_{j}\right].
\end{displaymath}](img165.gif) |
(67) |
Nun soll der Erwartungswert des Mittels einer Zeitreihe aus stationärem
Rauschen mit dem Erwartungswert 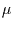 betrachtet werden.
Es gilt
betrachtet werden.
Es gilt
![\begin{displaymath}
E\left[\overline{x}^{N}\right]
= E\left[\frac{1}{N}\sum\l...
...
\frac{1}{N}\sum\limits_{i=1}^{N} E\left[x_{i}\right] = \mu.
\end{displaymath}](img167.gif) |
(68) |
Mit diesen ausführlichen Betrachtungen ist man nun in der Lage, die
Varianz des Mittelwerts über die Kovarianz der Zeitreihenwerte zu
formulieren.
Für die Varianz des Mittelwerts folgt durch Einsetzen von Glg. (62)
in Glg. (64)
![\begin{displaymath}
\mbox{var}\left[\frac{1}{N}\sum\limits_{i=1}^{N} x_{i}\righ...
...E\left[\sum\limits_{j=1}^{N} x_{j}\right]}_{\beta}
\right\}.
\end{displaymath}](img168.gif) |
(69) |
Nun ist
![\begin{displaymath}
\beta =\left(\sum\limits_{i=1}^{N}E[x_{i}]\right)\,
\left(\sum\limits_{j=1}^{N}E[x_{j}]\right)\,
\end{displaymath}](img169.gif) |
(70) |
und
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = & E\left[
\sum\limits_{i=1}...
...imits_{j=1}^{N}\,
E\left[x_{i}\,x_{j} \right].
\end{array}
\end{displaymath}](img170.gif) |
(71) |
Nach Glg. (67) folgt daraus wiederum
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = & \sum\limits_{i=1}^{N}\sum\...
...its_{j=1}^{N}\,\mbox{cov}[x_{i},x_{j}]
+ \beta.
\end{array}
\end{displaymath}](img171.gif) |
(72) |
Damit folgt für die Varianz der Mittelwerte die gesuchte Gleichung
![\begin{displaymath}
\mbox{var}\left[\frac{1}{N}\sum\limits_{i=1}^{N} x_{i}\righ...
...}^{N}\sum\limits_{j=1}^{N}\,\mbox{cov}[x_{i},x_{j}]\right).
\end{displaymath}](img172.gif) |
(73) |


Nächste Seite: Über dieses Dokument ...
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Ergebnisse
ich
2000-01-24
![\begin{displaymath}
E[X] =\lim\limits_{N\to\infty}\frac{1}{N} \sum\limits_{i=1}^{N}x_{i},
\end{displaymath}](img156.gif)
![\begin{displaymath}
E\left[\overline{x}^{N}\right]
= E\left[\frac{1}{N}\sum\l...
...
\frac{1}{N}\sum\limits_{i=1}^{N} E\left[x_{i}\right] = \mu.
\end{displaymath}](img167.gif)
![\begin{displaymath}
\mbox{var}\left[\frac{1}{N}\sum\limits_{i=1}^{N} x_{i}\righ...
...E\left[\sum\limits_{j=1}^{N} x_{j}\right]}_{\beta}
\right\}.
\end{displaymath}](img168.gif)
![\begin{displaymath}
\beta =\left(\sum\limits_{i=1}^{N}E[x_{i}]\right)\,
\left(\sum\limits_{j=1}^{N}E[x_{j}]\right)\,
\end{displaymath}](img169.gif)
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = & E\left[
\sum\limits_{i=1}...
...imits_{j=1}^{N}\,
E\left[x_{i}\,x_{j} \right].
\end{array}
\end{displaymath}](img170.gif)
![\begin{displaymath}
\begin{array}{rcl}
\alpha & = & \sum\limits_{i=1}^{N}\sum\...
...its_{j=1}^{N}\,\mbox{cov}[x_{i},x_{j}]
+ \beta.
\end{array}
\end{displaymath}](img171.gif)