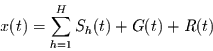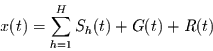

Nächste Seite: Einfluß der Mittelung auf
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Einleitung
Um von Zeitreihen von Monatsmitteln auf die statistischen Eigenschaften
von Zeitreihen von Tagesdaten schließen zu können,
gehen wir zunächst von einer allgemeinen zeitkontinuierlichen
Formulierung der Variable 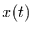 aus. Das bedeutet, daß die Untersuchung
auf Zeitreihen von Variablen beschränkt ist, die als zeitkontinuierlich
aufgefaßt werden können. Beispiele dafür sind der Luftdruck, die Feuchte,
die Windgeschwindigkeit und die Tagesmitteltemperatur.
Nicht zeitkontinuierliche Variablen, das sind z.B. alle Zeitreihen von
Ereignissen, wie Stürme und Hochwasser
können mit dieser Herangehensweise nicht untersucht werden.
In einem weiteren Schritt wird angenommen, daß die zu untersuchende Variable
als Überlagerung von
aus. Das bedeutet, daß die Untersuchung
auf Zeitreihen von Variablen beschränkt ist, die als zeitkontinuierlich
aufgefaßt werden können. Beispiele dafür sind der Luftdruck, die Feuchte,
die Windgeschwindigkeit und die Tagesmitteltemperatur.
Nicht zeitkontinuierliche Variablen, das sind z.B. alle Zeitreihen von
Ereignissen, wie Stürme und Hochwasser
können mit dieser Herangehensweise nicht untersucht werden.
In einem weiteren Schritt wird angenommen, daß die zu untersuchende Variable
als Überlagerung von 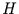 harmonischen
Anteilen
harmonischen
Anteilen 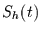 (z.B. dem mittleren Jahresgang, aber auch andere
harmonische Anteile), einer glatten nichtharmonischen Komponente
(z.B. dem mittleren Jahresgang, aber auch andere
harmonische Anteile), einer glatten nichtharmonischen Komponente 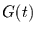 (z.B. ein linearer oder nichtlinearer Trend und episodische Schwankungen)
und einem Rauschen
(z.B. ein linearer oder nichtlinearer Trend und episodische Schwankungen)
und einem Rauschen 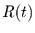 (dem Wetter) betrachtet werden kann. Es soll also
(dem Wetter) betrachtet werden kann. Es soll also
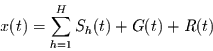 |
(1) |
gelten.
Dabei kann jeder harmonische Anteil in der Form
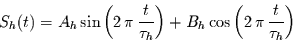 |
(2) |
ausgedrückt werden, was einer Schwingung
mit der Amplitude
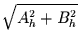 ,
der Periode
,
der Periode 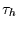 und der
Phasenlage
und der
Phasenlage
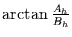 entspricht.
Das Rauschen kann zunächst die Realisation eines beliebigen
stochastischen Prozesses sein.
Mittelt man nun diese zeitliche Struktur zu einem beliebigen Zeitpunkt
entspricht.
Das Rauschen kann zunächst die Realisation eines beliebigen
stochastischen Prozesses sein.
Mittelt man nun diese zeitliche Struktur zu einem beliebigen Zeitpunkt
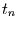 über ein darum zentriertes Intervall der
Länge
über ein darum zentriertes Intervall der
Länge 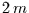 , so erhält man formal
, so erhält man formal
Man erkennt daraus, daß die Aufteilung der zeitkontinuierlichen
Variable 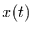 in deterministische Komponenten und Rauschen auch in den
Mittelwerten erhalten bleibt, was der bekannten Tatsache entspricht, daß
Summation und Mittelung in ihrer Reihenfolge austauschbare Operationen sind.
Dies erlaubt es, den Einfluß
jeder Komponente einzeln zu untersuchen, um die Ergebnisse am Ende wieder
zusammenzufügen. Im folgenden Abschnitt wird daher zunächst
der Einfluß der
Mittelung auf den harmonischen Anteil beschrieben. Im darauf folgenden
Abschnitt wird der Einfluß der Mittelung auf einige mögliche Arten der
glatten Komponente analysiert, bevor im Abschnitt
5 der Einfluß der Mittelung auf das Rauschen untersucht wird.
in deterministische Komponenten und Rauschen auch in den
Mittelwerten erhalten bleibt, was der bekannten Tatsache entspricht, daß
Summation und Mittelung in ihrer Reihenfolge austauschbare Operationen sind.
Dies erlaubt es, den Einfluß
jeder Komponente einzeln zu untersuchen, um die Ergebnisse am Ende wieder
zusammenzufügen. Im folgenden Abschnitt wird daher zunächst
der Einfluß der
Mittelung auf den harmonischen Anteil beschrieben. Im darauf folgenden
Abschnitt wird der Einfluß der Mittelung auf einige mögliche Arten der
glatten Komponente analysiert, bevor im Abschnitt
5 der Einfluß der Mittelung auf das Rauschen untersucht wird.


Nächste Seite: Einfluß der Mittelung auf
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Einleitung
ich
2000-01-24