

Nächste Seite: Ergebnisse
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Mittelung bei polynomialen Komponenten
Varianz des Rauschens der Monatsmittel und des
Rauschens der Tagesdaten
Um die Varianz des Rauschens in den Monatsmitteln
mit der Varianz des Rauschens der Tagesmittelwerte in
Verbindung zu bringen, wird nicht von einem zeitkontinuierlichen
Rauschen ausgegangen, da dies mit unnötigen und imensen Komplikationen
verbunden wäre. Stattdessen wird von einem zeitlich diskreten Rauschen
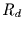 in den Tagesdaten ausgegangen, dessen Eigenschaften aus
Monatsmitteln rekonstruiert werden sollen.
Dabei sind die Tage mit dem Laufindex
in den Tagesdaten ausgegangen, dessen Eigenschaften aus
Monatsmitteln rekonstruiert werden sollen.
Dabei sind die Tage mit dem Laufindex 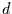 durchnummeriert.
Der Mittelwert über
durchnummeriert.
Der Mittelwert über 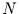 Tage ist dann gegeben durch
Tage ist dann gegeben durch
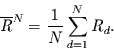 |
(45) |
Für die Varianz des Mittelwertes gilt dann
![\begin{displaymath}
\mbox{var}[\overline{R}^{N}] =
\mbox{var}[\frac{1}{N}\sum\limits_{d=1}^{N} R_{d}]
\end{displaymath}](img121.gif) |
(46) |
und nach Gleichung (73) weiter
![\begin{displaymath}
\mbox{var}[\overline{R}^{N}] =
\frac{1}{N^{2}}\sum\limits...
...u=1}^{N}\sum\limits_{j=1}^{N}
\mbox{cov}(R_{\tau},R_{j}).
\end{displaymath}](img122.gif) |
(47) |
Die Doppelsumme kann nun umsortiert werden zu
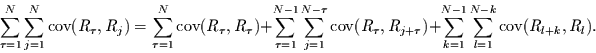 |
(48) |
Falls 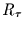 nun ein kovarianzstationäres Zufallsrauschen ist,
vereinfacht sich die Kovarianzfunktion
nun ein kovarianzstationäres Zufallsrauschen ist,
vereinfacht sich die Kovarianzfunktion
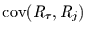 zu
zu
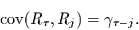 |
(49) |
Die Doppelsumme in Glg. (48) kann dann unter Nutzung von
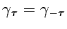 vereinfacht werden zu
vereinfacht werden zu
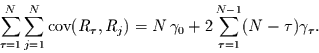 |
(50) |
Setzt man dies nun in Glg. (47) ein, so erhält man
![\begin{displaymath}
\fbox{$\displaystyle \mbox{var}[\overline{R}^{N}] =
\frac...
...ts_{\tau=1}^{N-1} \frac{N-\tau}{N}\,\gamma_{\tau}\right).$}
\end{displaymath}](img129.gif) |
(51) |
Diese Gleichung gibt nun den Zusammenhang zwischen der Varianz der Tagesdaten
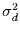 und der Varianz der Monatsmittel
und der Varianz der Monatsmittel
![$\mbox{var}[\overline{R}^{N}]$](img131.gif) an. Wesentlich ist dabei, daß man die
Autokovarianzfunktion des Rauschens der Tagesdaten kennen muß, um von der
Varianz der Monatsmittel auf die Varianz der Tagesmittel zu schließen.
Die Stärke des Einfusses der Autokovarianzfunktion der Tagesdaten auf den Zusammenhang
soll im Folgenden an einem Beispiel verdeutlicht werden.
Das Rauschen der Tagesdaten sei durch einen AR(1)-Prozeß, also durch die
Gleichung
an. Wesentlich ist dabei, daß man die
Autokovarianzfunktion des Rauschens der Tagesdaten kennen muß, um von der
Varianz der Monatsmittel auf die Varianz der Tagesmittel zu schließen.
Die Stärke des Einfusses der Autokovarianzfunktion der Tagesdaten auf den Zusammenhang
soll im Folgenden an einem Beispiel verdeutlicht werden.
Das Rauschen der Tagesdaten sei durch einen AR(1)-Prozeß, also durch die
Gleichung
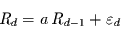 |
(52) |
mit dem Autoregressionskoeffizienten 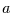 und dem Gaußschen weißen Rauschen
und dem Gaußschen weißen Rauschen
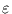 mit der Varianz
mit der Varianz
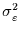 beschreibbar. Ein
Monat habe genau
beschreibbar. Ein
Monat habe genau 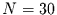 Tage.
Dann gilt für die Autokovarianzfunktion des Rauschens der Tagesdaten
bei der Zeitverschiebung
Tage.
Dann gilt für die Autokovarianzfunktion des Rauschens der Tagesdaten
bei der Zeitverschiebung 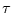
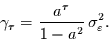 |
(53) |
Die Varianz der Tagesdaten ist dann
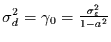 .
Bezeichnet man die Varianz der Monatsdaten mit
.
Bezeichnet man die Varianz der Monatsdaten mit
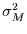 , so folgt
durch Einsetzen in Gleichung (51)
, so folgt
durch Einsetzen in Gleichung (51)
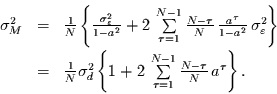 |
(54) |
Damit folgt für die Standardabweichung des Rauschens
der Tagesdaten als Funktion der
Standardabweichung des Rauschens der Monatsdaten
![\begin{displaymath}
\sigma_{d} = \sqrt{30} \,\sigma_{M} \left[
1 +2 \,\sum\lim...
...}^{29}
\frac{30-\tau}{30}\,a^{\tau}
\right]^{\frac{-1}{2}}.
\end{displaymath}](img140.gif) |
(55) |
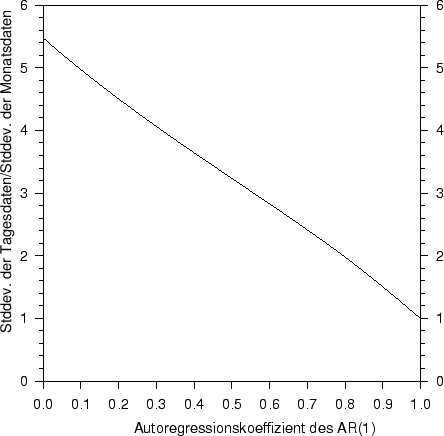
Für Autoregressionskoeffizienten zwischen 0 und 1 ist 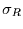 als
Funktion von
als
Funktion von 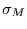 in Abbildung 2 dargestellt.
Im Grenzfall
in Abbildung 2 dargestellt.
Im Grenzfall 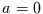 geht der AR(1)-Prozeß in ein weißes Rauschen über
und es folgt für die Standardabweichungen der unterschiedlich
gemittelten Zeitreihen der Zusammenhang
geht der AR(1)-Prozeß in ein weißes Rauschen über
und es folgt für die Standardabweichungen der unterschiedlich
gemittelten Zeitreihen der Zusammenhang
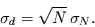 |
(56) |
Im Grenzfall 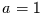 geht der stationäre AR(1)-Prozeß in den instationären
Brownschen Prozeß über. Dann ist die Varianz der Mittelwerte über
beliebige Zeiträume gleich der Varianz der ungemittelten Reihe.
Dies kann man leicht einsehen, indem man
geht der stationäre AR(1)-Prozeß in den instationären
Brownschen Prozeß über. Dann ist die Varianz der Mittelwerte über
beliebige Zeiträume gleich der Varianz der ungemittelten Reihe.
Dies kann man leicht einsehen, indem man 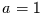 in Gleichung
(54) einsetzt. (Man beachte, daß für
in Gleichung
(54) einsetzt. (Man beachte, daß für 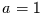 keine Autokovarianz
mehr definiert werden kann, da Glg. (53) dort eine Polstelle hat. Genaugenommen
betrachten wir hier also den Grenzfall
keine Autokovarianz
mehr definiert werden kann, da Glg. (53) dort eine Polstelle hat. Genaugenommen
betrachten wir hier also den Grenzfall 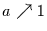 .)
Dann folgt
.)
Dann folgt
![\begin{displaymath}
\begin{array}{rcl}
\sigma_{M}^{2} & = &
\frac{1}{N} \sig...
...(N-1)}{2}\right\}\\ [1ex]
& = & \sigma_{d}^{2}.
\end{array}
\end{displaymath}](img147.gif) |
(57) |
Abbildung:
Abhängigkeit der Standardabweichung des Rauschens der
Tagesdaten als Vielfaches
der Standardabweichung der Monatsdaten falls die Tagesdaten
aus einem AR(1)-Prozeß mit dem Autoregressionskoeffizient 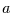 stammen.
stammen.
 |


Nächste Seite: Ergebnisse
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Mittelung bei polynomialen Komponenten
ich
2000-01-24
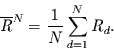
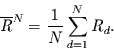
![\begin{displaymath}
\mbox{var}[\overline{R}^{N}] =
\mbox{var}[\frac{1}{N}\sum\limits_{d=1}^{N} R_{d}]
\end{displaymath}](img121.gif)
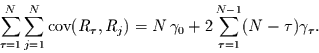
![\begin{displaymath}
\sigma_{d} = \sqrt{30} \,\sigma_{M} \left[
1 +2 \,\sum\lim...
...}^{29}
\frac{30-\tau}{30}\,a^{\tau}
\right]^{\frac{-1}{2}}.
\end{displaymath}](img140.gif)
![\begin{displaymath}
\begin{array}{rcl}
\sigma_{M}^{2} & = &
\frac{1}{N} \sig...
...(N-1)}{2}\right\}\\ [1ex]
& = & \sigma_{d}^{2}.
\end{array}
\end{displaymath}](img147.gif)
