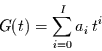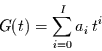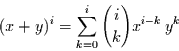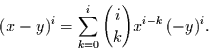

Nächste Seite: Varianz des Rauschens der
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Mittelung bei exponentiellem Trend
Falls die glatte Komponente einem Polynom der Art
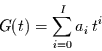 |
(36) |
entspricht, kann man jeden Summanden einzeln betrachten, da Mittelung und
Summation in der Reihenfolge austauschbar sind. Deshalb reicht es aus
eine Funktion der Art 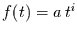 zu untersuchen.
Dazu muß erneut die Stammfunktion
zu untersuchen.
Dazu muß erneut die Stammfunktion
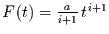 in Glg. (31) eingesetzt werden.
Dies führt zu
in Glg. (31) eingesetzt werden.
Dies führt zu
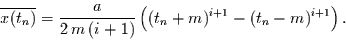 |
(37) |
Allgemein gilt
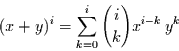 |
(38) |
und demnach auch
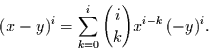 |
(39) |
Dann ist
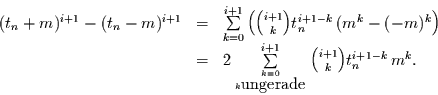 |
(40) |
Der Verlauf der Mittelwerte hat demnach die Form
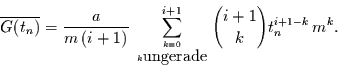 |
(41) |
Man kann durch Einsetzen leicht zeigen, daß für 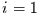 die bereits
angegebene Lösung für den Fall des linearen Trends entsteht.
Für
die bereits
angegebene Lösung für den Fall des linearen Trends entsteht.
Für 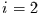 (also eine parabelförmige Komponente) hat die Summe in Glg.
(41) zwei Komponenten. Durch Einsetzen findet man
(also eine parabelförmige Komponente) hat die Summe in Glg.
(41) zwei Komponenten. Durch Einsetzen findet man
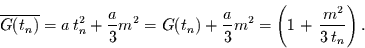 |
(42) |
Dabei stellt der Term ganz rechts in der Klammer den Fehler dar.
Dieser ist zu vernachlässigen, falls
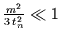 ist. Bei Mittelungsintervallen von einem
Monat, hat man z.B. nach zwei Monaten nur noch einen Fehler von
ist. Bei Mittelungsintervallen von einem
Monat, hat man z.B. nach zwei Monaten nur noch einen Fehler von 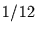 .
Für
.
Für
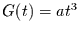 erhält man aus Glg. (41)
erhält man aus Glg. (41)
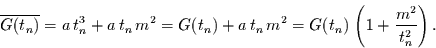 |
(43) |
Für
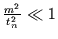 ist auch hier
der Fehler vernachlässigbar.
Als letztes Beispiel sei noch der Fall
ist auch hier
der Fehler vernachlässigbar.
Als letztes Beispiel sei noch der Fall
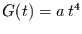 genannt, für den
aus Glg. (41) folgt
genannt, für den
aus Glg. (41) folgt
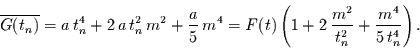 |
(44) |
Man sieht, wie bei den anderen untersuchten
Termen, daß für 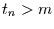 der Fehler sehr schnell gegen null geht.
Diese Eigenschaft erlaubt es i.a.
beliebige polynomiale Komponenten anhand von
Mittelwerten zu untersuchen und die gefundenen Ergebnisse ohne explizite
Korrektur auf die zeitkontinuierliche Variable zu übertragen.
Demzufolge können auch in Monatsmitteln gefundene polynomiale Komponenten
auf Tagesdaten übertragen werden.
der Fehler sehr schnell gegen null geht.
Diese Eigenschaft erlaubt es i.a.
beliebige polynomiale Komponenten anhand von
Mittelwerten zu untersuchen und die gefundenen Ergebnisse ohne explizite
Korrektur auf die zeitkontinuierliche Variable zu übertragen.
Demzufolge können auch in Monatsmitteln gefundene polynomiale Komponenten
auf Tagesdaten übertragen werden.


Nächste Seite: Varianz des Rauschens der
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Mittelung bei exponentiellem Trend
ich
2000-01-24