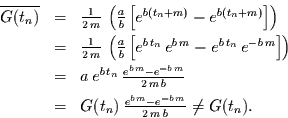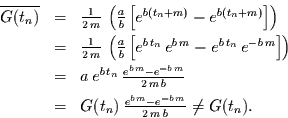

Nächste Seite: Mittelung bei polynomialen Komponenten
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Mittelung bei linearem Trend
Geht man davon aus, daß die glatte Komponente eine Exponentialfunktion
der Art
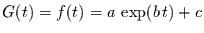 ist, so kann der konstante Term
ist, so kann der konstante Term 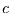 vernachlässigt werden, da bei der Untersuchung des linearen Trends
schon gezeigt wurde, daß er von der Mittelung unbeeinflußt bleibt.
Dann folgt die Stammfunktion
vernachlässigt werden, da bei der Untersuchung des linearen Trends
schon gezeigt wurde, daß er von der Mittelung unbeeinflußt bleibt.
Dann folgt die Stammfunktion
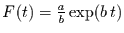 , die wiederum in
Glg. (31) einzusetzen ist.
Dies führt zu
, die wiederum in
Glg. (31) einzusetzen ist.
Dies führt zu
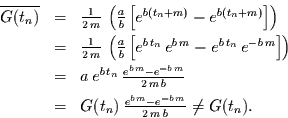 |
(33) |
Demnach wird ein exponentieller Trend in kontinuierlicher Zeit zwar durch
einen exponentiellen Trend in den Mittelwerten wiedergegeben, letzterer ist
aber um den Faktor
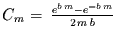 gegenüber dem
Original verändert. Je größer das Produkt
gegenüber dem
Original verändert. Je größer das Produkt 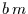 ist, desto größer
wird der Einfluß der Mittelung. Er ist aber bei der Trendbestimmung aus
Mittelwerten immer korrigierbar durch
ist, desto größer
wird der Einfluß der Mittelung. Er ist aber bei der Trendbestimmung aus
Mittelwerten immer korrigierbar durch
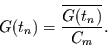 |
(34) |
Falls das Produkt 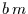 sehr klein ist, können die Exponentialfunktionen
in
sehr klein ist, können die Exponentialfunktionen
in 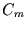 linearisiert werden, was zu
linearisiert werden, was zu
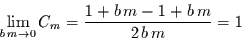 |
(35) |
führt. In diesem Grenzfall hat die Mittelbildung keinen Einfluß mehr.


Nächste Seite: Mittelung bei polynomialen Komponenten
Aufwärts: Einfluß der Mittelung auf
Vorherige Seite: Mittelung bei linearem Trend
ich
2000-01-24