

Nächste Seite: Mittelung bei linearem Trend
Aufwärts: Was sagen Monatsmittelwerte über
Vorherige Seite: Quadratische Amplitudenfunktion
Um den Einfluß der Mittelung auf glatte Komponenten einer (in der Zeit
kontinuierlichen) Variable zu untersuchen, wird angenommen, daß diese
in der Form von integrierbaren
Funktionen 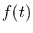 ausgedrückt werden können.
Es sei also
ausgedrückt werden können.
Es sei also 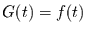 . Dann gilt für den Mittelwert über das
Intervall
. Dann gilt für den Mittelwert über das
Intervall 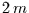 um den Zeitpunkt
um den Zeitpunkt 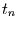
![\begin{displaymath}
\overline{G(t_{n})}=\frac{1}{2\,m}\int\limits_{t_{n}-m}^{t_...
...\,dt =
\frac{1}{2\,m}\left[F(t_{n}+m) - F(t_{n}-m)\right],
\end{displaymath}](img82.gif) |
(31) |
wenn 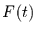 die Stammfunktion von
die Stammfunktion von 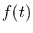 bezeichnet.
Ein Vergleich von
bezeichnet.
Ein Vergleich von
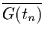 und
und 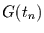 zeigt dann, wie
der Verlauf der glatten Komponente durch den
Prozeß der Mittelung verändert wurde.
Dazu sollen nun drei Beispiele besprochen werden.
zeigt dann, wie
der Verlauf der glatten Komponente durch den
Prozeß der Mittelung verändert wurde.
Dazu sollen nun drei Beispiele besprochen werden.
Unterabschnitte
ich
2000-01-24
![\begin{displaymath}
\overline{G(t_{n})}=\frac{1}{2\,m}\int\limits_{t_{n}-m}^{t_...
...\,dt =
\frac{1}{2\,m}\left[F(t_{n}+m) - F(t_{n}-m)\right],
\end{displaymath}](img82.gif)