

Nächste Seite: Über dieses Dokument ...
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Bayes-Schätzer für
Die Bayes'sche Formel (der Bayes'sche Satz, das Bayes'sche Theorem) hat Thomas
Bayes (1701-1761 und Schüler von de Moivre) im Jahre 1750 entdeckt. Sie wurde
trotzdem erst nach seinem Tod veröffentlicht. Da Bayes sich nicht mehr gegen
die Kritik daran wehren konnte, schlimmer noch, nicht für seine Formel werben
konnte, wurde sie nicht weiter beachtet, bis sie gegen Ende des 20. Jh im
Zusammenhang mit der Parameterschätzung interessant wurde. Seitdem scheinen
die Statistiker in zwei Lager gespalten zu sein: den Bayesianern und den
Anti-Bayesianern (siehe z.B. Szekely, 1990). Frei von der sich immer weiter
vertiefenden Kluft (Szekely, 1990) zwischen diesen beiden Lagern scheinen
die deutschen Statistiker zu sein, die zwar in ihren Lehrbüchern auf die
Existenz der Bayes'schen Formel aufmerksam machen, weiter aber nichts damit
zu tun haben. Da mit Hilfe moderner Großrechenanlagen sehr aufwendige
Anwendungen der Bayes'schen Formel möglich werden und da diese auch in der
statistischen Klimatologie Anwendung finden, sollte man sich wenigstens grob
bewußt machen, wovon Bayesianer reden.
Um die Bayes'sche Formel abzuleiten gehen wir von zwei Zufallsvariablen 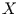 und
und 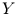 aus. Diese können jeweils Werte aus einem bestimmten Wertebereich
annehmen. Es existieren dann eindimensionale Wahrscheinlichkeitsdichten
dafür, daß
aus. Diese können jeweils Werte aus einem bestimmten Wertebereich
annehmen. Es existieren dann eindimensionale Wahrscheinlichkeitsdichten
dafür, daß 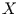 den Wert
den Wert 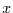 annimmt (
annimmt (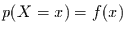 ) und dafür,
daß
) und dafür,
daß 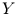 den Wert
den Wert 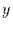 annimmt (
annimmt (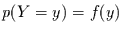 ). Zusätzlich kann
man die gemeinsame (zweidimensionale) Wahrscheinlichkeitsdichte
). Zusätzlich kann
man die gemeinsame (zweidimensionale) Wahrscheinlichkeitsdichte
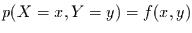 definieren. Falls es nun
zwischen den Zufallsvariablen
definieren. Falls es nun
zwischen den Zufallsvariablen 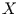 und
und 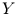 keinen Zusammenhang gibt, gilt
keinen Zusammenhang gibt, gilt
Andernfalls gilt
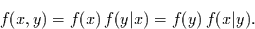 |
(16) |
In dieser nicht auf Anhieb einsichtigen Gleichung, stellen die Funktionen
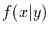 und
und 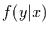 bedingte Wahrscheinlichkeiten dar. Dabei bedeutet
bedingte Wahrscheinlichkeiten dar. Dabei bedeutet
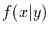 die Wahrscheinlichkeit dafür, daß die Variable
die Wahrscheinlichkeit dafür, daß die Variable 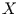 den Wert
den Wert 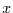 annimmt, wenn die Variable
annimmt, wenn die Variable 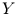 den Wert
den Wert 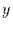 angenommen hat.
angenommen hat. 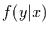 ist
demnach genau umgekehrt definiert. Also sagt Gleichung (16) aus, daß
die Wahrscheinlichkeit dafür, daß
ist
demnach genau umgekehrt definiert. Also sagt Gleichung (16) aus, daß
die Wahrscheinlichkeit dafür, daß 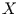 den Wert
den Wert 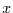 und
und 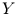 den Wert
den Wert 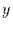 annimmt (
annimmt (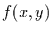 ), gegeben ist durch die Wahrscheinlichkeit, mit der
), gegeben ist durch die Wahrscheinlichkeit, mit der 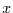 realisiert wird (
realisiert wird (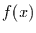 )
mal der Wahrscheinlichkeit, daß
)
mal der Wahrscheinlichkeit, daß 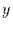 realisiert wird, wenn
realisiert wird, wenn 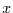 realisiert wird
(
realisiert wird
(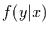 ). Das Gleiche gilt natürlich auch, wenn man
). Das Gleiche gilt natürlich auch, wenn man 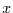 und
und 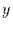 vertauscht. Nun kann Gleichung (16) dazu verwendet werden bedingte
Wahrscheinlichkeiten zu invertieren, denn es folgt sofort
vertauscht. Nun kann Gleichung (16) dazu verwendet werden bedingte
Wahrscheinlichkeiten zu invertieren, denn es folgt sofort
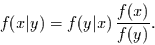 |
(17) |
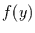 kann noch etwas weiter verändert werden.
Im Fall von diskreten Variablen
kann noch etwas weiter verändert werden.
Im Fall von diskreten Variablen 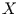 und
und 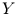 summiert man den rechten Teil von
Gleichung (16) über alle möglichen Werte von
summiert man den rechten Teil von
Gleichung (16) über alle möglichen Werte von 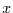 und erhält wegen
und erhält wegen
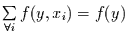
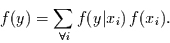 |
(18) |
Diese Gleichung besagt, daß die Wahrscheinlichkeit, daß die Zufallsvariable
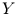 den Wert
den Wert 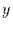 annimmt, aus der Summe der bedingten Wahrscheinlichkeiten
für
annimmt, aus der Summe der bedingten Wahrscheinlichkeiten
für 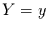 unter der Bedingung
unter der Bedingung 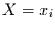 folgt. Dabei muß die Summe über
alle möglichen Realisierungen von
folgt. Dabei muß die Summe über
alle möglichen Realisierungen von 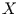 (d.h. alle
(d.h. alle 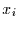 ) laufen. Da
Gleichung (18) die vollständige Wahrscheinlichkeit als Summe von
Einzelwahrscheinlichkeiten beschreibt, wird sie in der Literatur oft als Satz
von der vollständigen Wahrscheinlichkeit eingeführt.
Setzt man nun Gleichung (18) in Gleichung (17) ein, so erhält man
die Bayes'sche Formel für diskrete Zufallsvariable:
) laufen. Da
Gleichung (18) die vollständige Wahrscheinlichkeit als Summe von
Einzelwahrscheinlichkeiten beschreibt, wird sie in der Literatur oft als Satz
von der vollständigen Wahrscheinlichkeit eingeführt.
Setzt man nun Gleichung (18) in Gleichung (17) ein, so erhält man
die Bayes'sche Formel für diskrete Zufallsvariable:
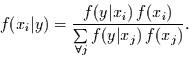 |
(19) |
In analoger Weise kann man für kontinueierliche Wertebereiche den Satz von
der vollständigen Wahrscheinlichkeit formulieren
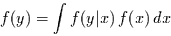 |
(20) |
und daraus die Bayes'sche
Formel für kontinuierliche Zufallsvariable
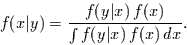 |
(21) |
Manche Autoren (z.B.) Hsu (1996) nennen Gleichung (17) Bayes'sche Regel
und die Gleichungen (19) und (21) Bayes'sches Theorem.


Nächste Seite: Über dieses Dokument ...
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Bayes-Schätzer für
ich
2000-01-24