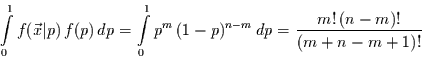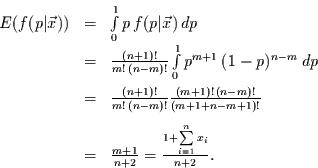

Nächste Seite: Anhang: Bayes'sche Formel
Aufwärts: Ein Beispiel zum Vergleich
Vorherige Seite: ML-Schätzer für
Um den Bayes-Schätzer für 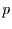 angeben zu können, braucht man zunächst
einen Prior. Da man über
angeben zu können, braucht man zunächst
einen Prior. Da man über 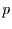 keine Information vorraussetzen kann, nimmt man
(nicht zuletzt auch der Einfachheit halber)
keine Information vorraussetzen kann, nimmt man
(nicht zuletzt auch der Einfachheit halber) 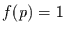 für alle Werte von
für alle Werte von 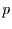 zwischen
zwischen 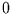 und
und 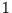 an. Für den Posterior folgt dann nach Gleichung
(4)
an. Für den Posterior folgt dann nach Gleichung
(4)
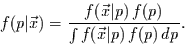 |
(13) |
Dabei ist
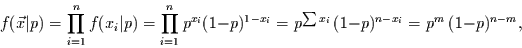 |
(14) |
mit 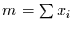 die Likelihood-Funktion.
Für das Integral im Nenner von Gleichung (13) folgt dann
die Likelihood-Funktion.
Für das Integral im Nenner von Gleichung (13) folgt dann
und damit folgt durch Einsetzen in Gleichung (13)
Das ist nun der Posterior, der aus dem Prior 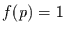 und der
Likelihood-Funktion folgt. Er gibt eine Wahrscheinlichkeitsverteilung für den
zu bestimmenden Koeffizienten an. Man sieht, daß man durch eine Normierung
der Likelihood-Funktion die gleiche Wahrscheinlichkeitsdichte auch bei der
ML-Anwendung erhalten hätte. Das ist aber nur in den seltenen Fällen so, in
denen der Prior eine Konstante ist. Nun müssen wir nur noch den
Erwartungswert
und der
Likelihood-Funktion folgt. Er gibt eine Wahrscheinlichkeitsverteilung für den
zu bestimmenden Koeffizienten an. Man sieht, daß man durch eine Normierung
der Likelihood-Funktion die gleiche Wahrscheinlichkeitsdichte auch bei der
ML-Anwendung erhalten hätte. Das ist aber nur in den seltenen Fällen so, in
denen der Prior eine Konstante ist. Nun müssen wir nur noch den
Erwartungswert
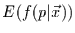 berechnen, der dann der Bayes-Schätzer für
den Parameter ist. (Man beachte, daß man, da man die Wahrscheinlichkeitsdichte
kennt, auch jedes beliebige Quantil (also auch Konfidenzintervalle) für den
Parameter berechnen kann.)
berechnen, der dann der Bayes-Schätzer für
den Parameter ist. (Man beachte, daß man, da man die Wahrscheinlichkeitsdichte
kennt, auch jedes beliebige Quantil (also auch Konfidenzintervalle) für den
Parameter berechnen kann.)
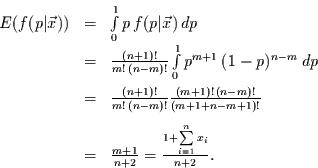 |
(15) |
Für das gewählte Zahlenbeispiel folgt daraus der Bayes-Schätzer
Dem aufmerksamen Leser müßte jetzt nicht nur aufgefallen sein, daß
sich
diese beiden Schätzer unterscheiden (der Unterschied wird für große 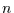 allerdings beliebig klein), sondern auch warum sie sich unterscheiden.
Während der ML-Schätzer den wahrscheinlichsten Wert, d.h. den mit der
höchsten Wahrscheinlichkeitsdichte, also den Modalwert der
Wahrscheinlichkeitsverteilung für den Parameterwert auswählt, wählt der
Bayes-Schätzer den Erwartungswert.
allerdings beliebig klein), sondern auch warum sie sich unterscheiden.
Während der ML-Schätzer den wahrscheinlichsten Wert, d.h. den mit der
höchsten Wahrscheinlichkeitsdichte, also den Modalwert der
Wahrscheinlichkeitsverteilung für den Parameterwert auswählt, wählt der
Bayes-Schätzer den Erwartungswert.


Nächste Seite: Anhang: Bayes'sche Formel
Aufwärts: Ein Beispiel zum Vergleich
Vorherige Seite: ML-Schätzer für
ich
2000-01-24