

Nächste Seite: Ein Beispiel zum Vergleich
Aufwärts: Schätzverfahren
Vorherige Seite: Maximum-Likelihood-Schätzer
Bayes-Schätzer basieren auf der Bayes'schen Formel (siehe Anhang). Dabei
wird nicht nur der
Erwartungswert eines Parameters geschätzt, sondern dieser als Zufallsvariable
aufgefaßt und deren Verteilung geschätzt. Kennt man die Verteilung, so
hat man alle verfügbare Information über den Parameter.
Setzt man in Gleichung (21) für die Zufallsvariable 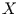 den Parameter
den Parameter
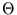 ein und für
ein und für 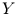 die
die 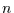 -dimensionale Stichprobe
-dimensionale Stichprobe 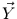 , so folgt
, so folgt
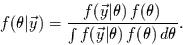 |
(4) |
Mit dieser Gleichung kann man aus einem Prior-Schätzer 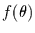 (der
z.B. mehr oder weniger gut geraten ist) über eine sogenannte
Likelihood-Funktion in Abhängigkeit von den Daten auf einen (womöglich aber
nicht notwendigerweise) besseren Posterior-Schätzer
(der
z.B. mehr oder weniger gut geraten ist) über eine sogenannte
Likelihood-Funktion in Abhängigkeit von den Daten auf einen (womöglich aber
nicht notwendigerweise) besseren Posterior-Schätzer
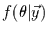 schließen. Dabei fällt auf, daß man dieses Verfahren sukzessive anwenden
kann, in der Hoffnung, daß es möglichst rasch und gegen einen richtigen
Posterior konvergiert. Andererseits muß man dann aber auch recht viele
Integrale ausführen.
Der Bayes-Schätzer für den gesuchten Parameter ist dann der Erwartungswert
der Posterior-Verteilung und ist gegeben durch das Integral
schließen. Dabei fällt auf, daß man dieses Verfahren sukzessive anwenden
kann, in der Hoffnung, daß es möglichst rasch und gegen einen richtigen
Posterior konvergiert. Andererseits muß man dann aber auch recht viele
Integrale ausführen.
Der Bayes-Schätzer für den gesuchten Parameter ist dann der Erwartungswert
der Posterior-Verteilung und ist gegeben durch das Integral
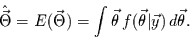 |
(5) |
Falls 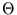 ein Parametervektor ist, d.h. falls man
mehrere Parameter zu schätzen hat, steht im Nenner von Gleichung (4)
ein Mehrfachintegral, daß in der Regel nur noch durch Monte-Carlo-Integration
gelöst werden kann.
Bayes-Schätzer können nicht nur dazu verwendet werden, um
Parameterwertverteilungen bei vorgegebenen Daten und angenommener Modellvorstellung
zu schätzen, sondern man kann auch Wahrscheinlichkeitsverteilungen für verschiedene
Modelltypen untersuchen.
Dies führt zu den Markov Chain Monte Carlo Methoden (MCMC). Dabei sind die
verschiedenen (vorzugebenden) konkurrierenden Modelle die diskreten Werte des
zu schätzenden Parameters (der Parameter ist in diesem Fall die Modellnummer).
Da jedes Modell wieder eine gewisse Anzahl von Modellparametern hat, muß bei
dieser Anwendung in verschiedenen (aber alternierenden) Stufen vorgegangen
werden. So hat man die Modellstufe mit der Gleichung
ein Parametervektor ist, d.h. falls man
mehrere Parameter zu schätzen hat, steht im Nenner von Gleichung (4)
ein Mehrfachintegral, daß in der Regel nur noch durch Monte-Carlo-Integration
gelöst werden kann.
Bayes-Schätzer können nicht nur dazu verwendet werden, um
Parameterwertverteilungen bei vorgegebenen Daten und angenommener Modellvorstellung
zu schätzen, sondern man kann auch Wahrscheinlichkeitsverteilungen für verschiedene
Modelltypen untersuchen.
Dies führt zu den Markov Chain Monte Carlo Methoden (MCMC). Dabei sind die
verschiedenen (vorzugebenden) konkurrierenden Modelle die diskreten Werte des
zu schätzenden Parameters (der Parameter ist in diesem Fall die Modellnummer).
Da jedes Modell wieder eine gewisse Anzahl von Modellparametern hat, muß bei
dieser Anwendung in verschiedenen (aber alternierenden) Stufen vorgegangen
werden. So hat man die Modellstufe mit der Gleichung
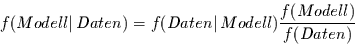 |
(6) |
und die Parameterstufe mit
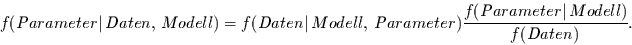 |
(7) |
Die Gleichungen (6) und (7) werden dann in einem Markov-Ketten-Lauf
alternierend verwendet, d.h. es wird versucht, das die Daten optimal beschreibende
Modell mit der optimalen Parameterkombination zu finden.
Eine solche Anwendung könnte man auch weniger automatisiert
(und meines Erachtens weniger aufwendig und klarer durchschaubar) realisieren,
indem man einige in Frage kommenden Modellstrukturen auswählt (z.B. einige
ARMA-Prozesse), diese alle optimal anpaßt, und dann die Güte miteinander
vergleicht. Da dabei Modelle mit mehr Parametern eine höhere Freiheit bei
der optimalen Anpassung haben, müßsen diese beim Vergleich etwas
benachteiligt werden. Dies geschieht unter Berücksichtigung eben dieser
Freiheitsgrade mit Hilfe verschiedener Kriterien (z.B.
Akaike-Informations-Kriterium, AIC).


Nächste Seite: Ein Beispiel zum Vergleich
Aufwärts: Schätzverfahren
Vorherige Seite: Maximum-Likelihood-Schätzer
ich
2000-01-24