

Nächste Seite: ML-Schätzer für
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Bayes-Schätzer
Gegeben sei ein Bernoulli-Experiment, d.h. ein Zufallsexperiment mit zwei
möglichen Ausgängen. Solche Experimente, für die der Münzwurf Pate stehen
muß, sind bei weitem nicht so unrealistisch, wie mancher hoffen mag.
Die beiden
Ausgänge des Experiments können durch 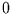 und
und 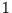 charakterisiert
werden. Die
charakterisiert
werden. Die 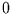 kann dann für das Nichteintreten eines Ereignisses, die
kann dann für das Nichteintreten eines Ereignisses, die 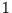 für dessen Eintreten stehen. Ereignisse können z.B. Treffer bei der
Wettervorhersage sein, Vulkanausbrüche, Tornados, aber auch Über-
bzw. Unterschreitungen von Schwellen bei beliebigen kontinuierlichen Variablen
sein. Aus der Beobachtung solcher Variablen möchte man dann die
Eintrittswahrscheinlichkeit
für dessen Eintreten stehen. Ereignisse können z.B. Treffer bei der
Wettervorhersage sein, Vulkanausbrüche, Tornados, aber auch Über-
bzw. Unterschreitungen von Schwellen bei beliebigen kontinuierlichen Variablen
sein. Aus der Beobachtung solcher Variablen möchte man dann die
Eintrittswahrscheinlichkeit 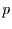 für das Ereignis
für das Ereignis 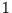 schätzen. Für die
Wahrscheinlichkeitsdichten muß
schätzen. Für die
Wahrscheinlichkeitsdichten muß 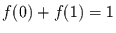 gelten. Mit
gelten. Mit 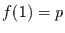 folgt
daraus sofort
folgt
daraus sofort 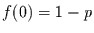 . Weiter gilt aber auch
. Weiter gilt aber auch
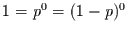 . Damit
kann man die sogenannte Bernoulli-Verteilung definieren:
. Damit
kann man die sogenannte Bernoulli-Verteilung definieren:
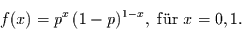 |
(8) |
Da diese Verteilung von dem (einen) Parameter 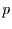 abhängt, wird eine
Realisation
abhängt, wird eine
Realisation 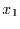 mit der Wahrscheinlichkeit
mit der Wahrscheinlichkeit 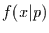 den Wert
den Wert 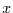 haben.
Nun betrachten wir eine Versuchsreihe mit
haben.
Nun betrachten wir eine Versuchsreihe mit 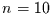 Realisationen:
Realisationen:
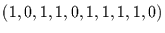 . Daraus soll der Parameter
. Daraus soll der Parameter 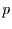 möglichst gut
geschätzt werden. Zunächst verwenden wir dazu den ML-Schätzer.
möglichst gut
geschätzt werden. Zunächst verwenden wir dazu den ML-Schätzer.
Unterabschnitte


Nächste Seite: ML-Schätzer für
Aufwärts: Anmerkungen zur Schätztheorie
Vorherige Seite: Bayes-Schätzer
ich
2000-01-24