

Nächste Seite: Bayes-Schätzer für
Aufwärts: Ein Beispiel zum Vergleich
Vorherige Seite: Ein Beispiel zum Vergleich
Die Likelihood-Funktion
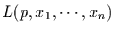 ist gegeben durch
ist gegeben durch
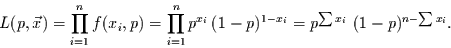 |
(9) |
Für das konkrete Zahlenbeispiel folgt damit
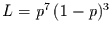 . Würde man
dies maximieren wollen, müßte man die Nullstellen der Ableitung
. Würde man
dies maximieren wollen, müßte man die Nullstellen der Ableitung 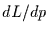 suchen. Im konkreten Fall also
suchen. Im konkreten Fall also
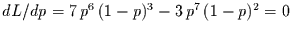 lösen. Der Grad des Polynoms, dessen Nullstellen man
zu finden hat steigt linear mit der Anzahl der Beobachtungsdaten. Deshalb
leitet man auch hier wieder die Loglikelihood-Funktion ab und sucht deren
Nullstellen:
lösen. Der Grad des Polynoms, dessen Nullstellen man
zu finden hat steigt linear mit der Anzahl der Beobachtungsdaten. Deshalb
leitet man auch hier wieder die Loglikelihood-Funktion ab und sucht deren
Nullstellen:
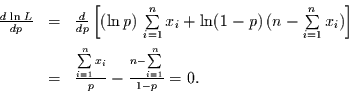 |
(10) |
Die Nullstellen dieser Gleichung lassen sich sehr einfach finden und es folgt
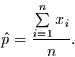 |
(11) |
Für das gewählte Zahlenbeispiel folgt daraus ein Wert von
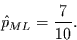 |
(12) |
ich
2000-01-24